publications

2024

1. 

   Breaking the left-right symmetry in fluttering artificial cilia that perform nonreciprocal oscillations

   Ariel Surya Boiardi, and Roberto Marchello

   Meccanica, 2024

   Abs DOI Bib

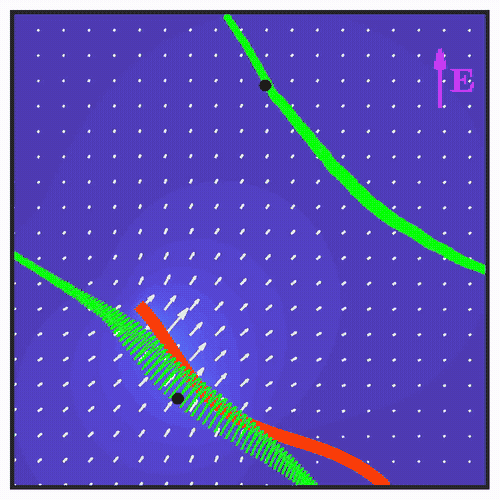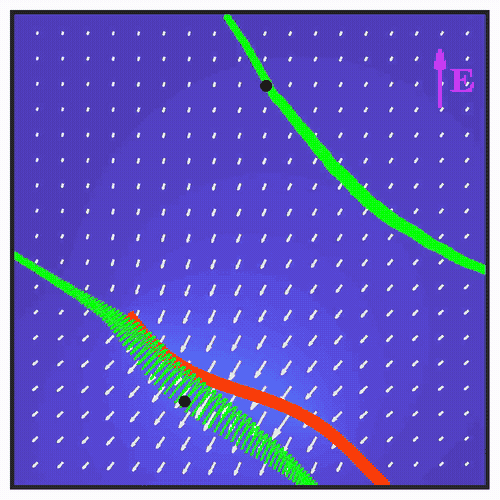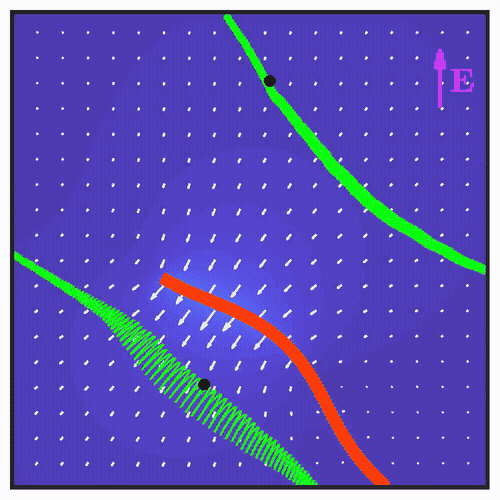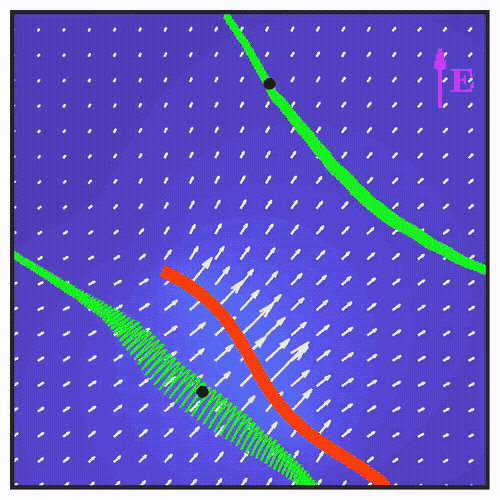
   Recent investigations on active materials have introduced a new paradigm for soft robotics by showing that a complex response can be obtained from simple stimuli by harnessing dynamic instabilities. In particular, polyelectrolyte hydrogel filaments actuated by a constant electric field have been shown to exhibit self-sustained oscillations as a consequence of flutter instability. Owing to the nonreciprocal nature of the emerging oscillations, these artificial cilia are able to generate flows along the stimulus. Building upon these findings, in this paper we propose a design strategy to break the left-right symmetry in the generated flows, by endowing the filament with a natural curvature at the fabrication stage. We develop a mathematical model based on morphoelastic rod theory to characterize the stability of the equilibrium configurations of the filament, proving the persistence of flutter instability. We show that the emerging oscillations are nonreciprocal and generate thrust at an angle with the stimulus. The results we find at the level of the single cilium open new perspectives on the possible applications of artificial ciliary arrays in soft robotics and microfluidics.

   @article{boiardi_breaking_2024,
     title = {Breaking the left-right symmetry in fluttering artificial cilia that perform nonreciprocal oscillations},
     issn = {1572-9648},
     url = {https://doi.org/10.1007/s11012-024-01765-7},
     doi = {10.1007/s11012-024-01765-7},
     journal = {Meccanica},
     shortjournal = {Meccanica},
     author = {Boiardi, Ariel Surya and Marchello, Roberto},
     urldate = {2024-06-11},
     year = {2024},
     langid = {english},
     keywords = {Artificial cilia, Flutter instability, Active matter, Left-right symmetry breaking, Soft-robotics},
   }

2. JMPS

   

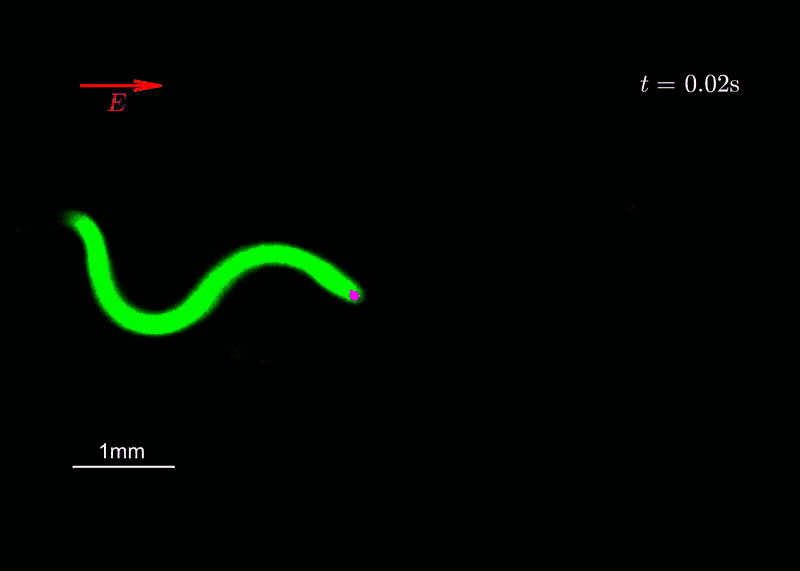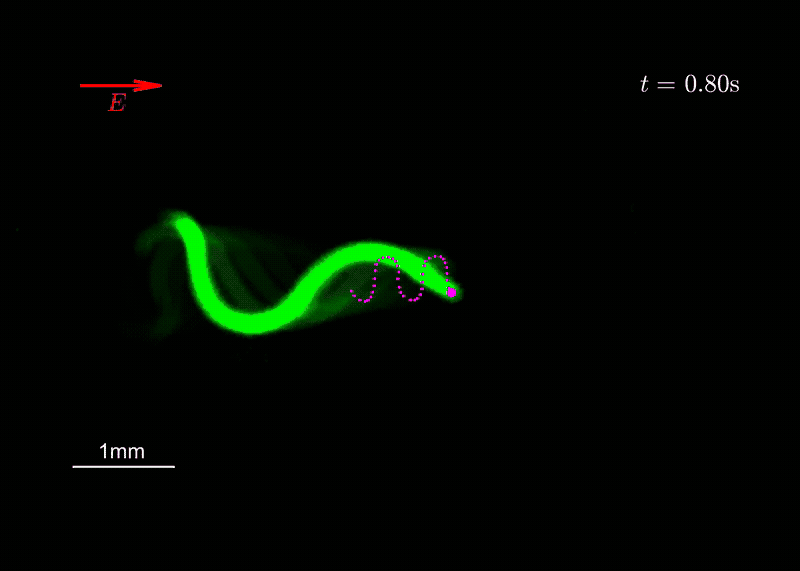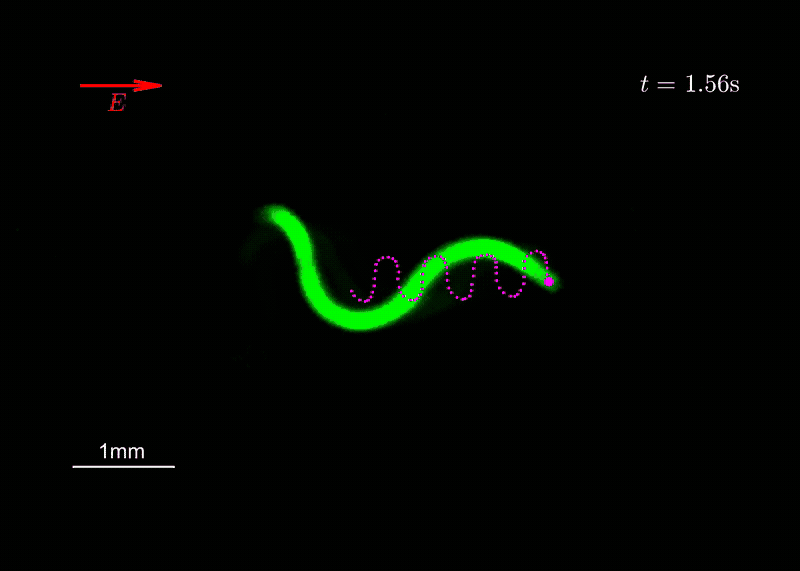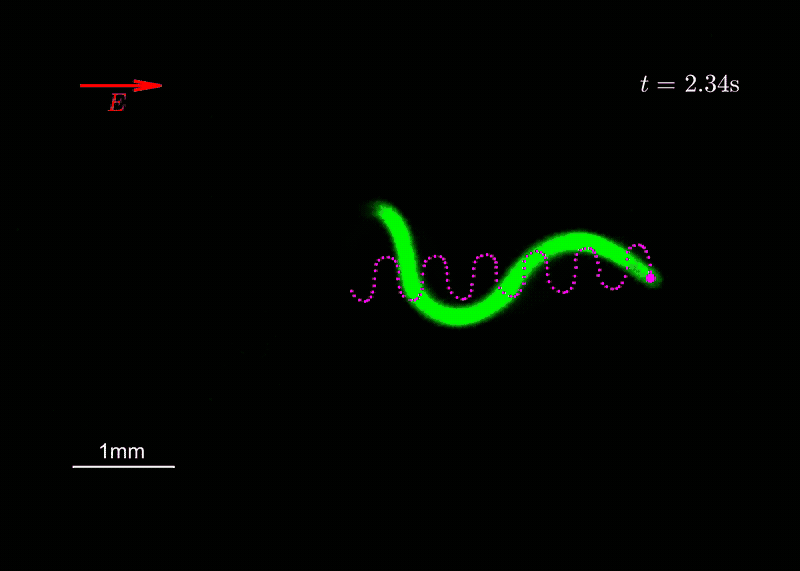   Minimal actuation and control of a soft hydrogel swimmer from flutter instability

   Ariel Surya Boiardi, and Giovanni Noselli

   Journal of the Mechanics and Physics of Solids, 2024

   Abs DOI Bib

   Micro-organisms propel themselves in viscous environments by the periodic, nonreciprocal beating of slender appendages known as flagella. Active materials have been widely exploited to mimic this form of locomotion. However, the realization of such coordinated beating in biomimetic flagella requires complex actuation modulated in space and time. We prove through experiments on polyelectrolyte hydrogel samples that directed undulatory locomotion of a soft robotic swimmer can be achieved by untethered actuation from a uniform and static electric field. A minimal mathematical model is sufficient to reproduce, and thus explain, the observed behavior. The periodic beating of the swimming hydrogel robot emerges from flutter instability thanks to the interplay between its active and passive reconfigurations in the viscous environment. Interestingly, the flutter-driven soft robot exhibits a form of electrotaxis whereby its swimming trajectory can be controlled by simply reorienting the electric field. Our findings trace the route for the embodiment of mechanical intelligence in soft robotic systems by the exploitation of flutter instability to achieve complex functional responses to simple stimuli. While the experimental study is conducted on millimeter-scale hydrogel swimmers, the design principle we introduce requires simple geometry and is hence amenable for miniaturization via micro-fabrication techniques. We believe it may also be transferred to a wider class of soft active materials.

   @article{boiardi_minimal_2024,
     title = {Minimal actuation and control of a soft hydrogel swimmer from flutter instability},
     volume = {191},
     issn = {0022-5096},
     url = {https://www.sciencedirect.com/science/article/pii/S0022509624002199},
     doi = {10.1016/j.jmps.2024.105753},
     pages = {105753},
     journal = {Journal of the Mechanics and Physics of Solids},
     shortjournal = {Journal of the Mechanics and Physics of Solids},
     author = {Boiardi, Ariel Surya and Noselli, Giovanni},
     urldate = {2024-07-07},
     year = {2024},
     keywords = {Flutter instability, Hopf bifurcation, Active materials, Polyelectrolyte hydrogels, Soft robotics},
   }

2022

1. M.Sc. Thesis

   

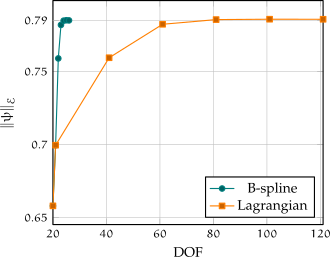   IGA-Energetic BEM: An Effective Tool for the Numerical Solution of Wave Propagation Problems in Space-Time Domain

   Alessandra Aimi, and Ariel Surya Boiardi

   Mathematics, 2022

   Abs DOI Bib

   The Energetic Boundary Element Method (BEM) is a recent discretization technique for the numerical solution of wave propagation problems, inside bounded domains or outside bounded obstacles. The differential model problem is converted into a Boundary Integral Equation (BIE) in the time domain, which is then written into an energy-dependent weak form successively discretized by a Galerkin-type approach. Taking into account the space-time model problem of 2D soft-scattering of acoustic waves by obstacles described by open arcs by B-spline (or NURBS) parametrizations, the aim of this paper is to introduce the powerful Isogeometric Analysis (IGA) approach into Energetic BEM for what concerns discretization in space variables. The same computational benefits already observed for IGA-BEM in the case of elliptic (i.e., static) problems, is emphasized here because it is gained at every step of the time-marching procedure. Numerical issues for an efficient integration of weakly singular kernels, related to the fundamental solution of the wave operator and dependent on the propagation wavefront, will be described. Effective numerical results will be given and discussed, showing, from a numerical point of view, convergence and accuracy of the proposed method, as well as the superiority of IGA-Energetic BEM compared to the standard version of the method, which employs classical Lagrangian basis functions.

   @article{aimi_iga-energetic_2022,
     title = {{IGA}-Energetic {BEM}: An Effective Tool for the Numerical Solution of Wave Propagation Problems in Space-Time Domain},
     volume = {10},
     rights = {http://creativecommons.org/licenses/by/3.0/},
     issn = {2227-7390},
     url = {https://www.mdpi.com/2227-7390/10/3/334},
     doi = {10.3390/math10030334},
     shorttitle = {{IGA}-Energetic {BEM}},
     pages = {334},
     number = {3},
     journal = {Mathematics},
     author = {Aimi, Alessandra and Boiardi, Ariel Surya},
     year = {2022},
     langid = {english},
     keywords = {energetic {BEM}, Isogeometric Analysis, soft-scattering, wave propagation},
   }