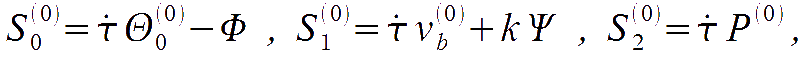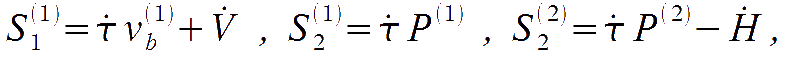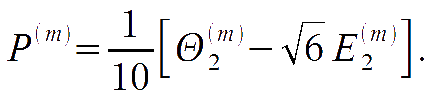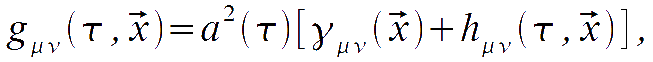
Cosmic Microwave Background Anisotropies
In these lectures we review the basic features of the Cosmic Microwave Background (CMB) anisotropies in linear regime. It is based on the linear cosmological perturbation theory (see Kodama & Sasaki, Progr. Theor. Phys. 78, 1, 1984). We follow the total angular momentum method for CMB anisotropies (Hu & White, Phys. Rev. D 56, 596, 1997); we describe the acoustic oscillations by casting it for spatially symmetric seed, spherical or cylindrical (Baccigalupi, Phys. Rev. D 59, 123004, 1999).
Linear Cosmological Perturbation Theory
Linear cosmological perturbations are defined as
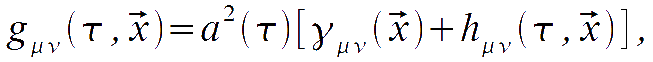
where the first term represents the unperturbed Friedmann Robertson Walker (FRW) metric with the conformal time defined as
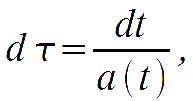
reducing to the ordinary Minkowski in flat geometry, clm; the second term represents the perturbation metric tensor, in linear regime:
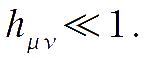
The perturbation metric tensor is conveniently expressed in the Fourier space. Due to gauge freedom, the independent perturbation quantities are two scalars and one vector; the tensor perturbation is gauge invariant. Before the definition of our relevant perturbation quantities, we define the suitable complete set of expansion in the Fourier space.
Scalar perturbations
A suitable expansion set is defined by the eigenfunctions of the Laplace operator:
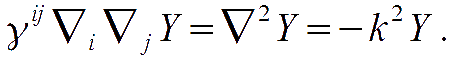
Their following functions describe scalar-type components of vector and tensor, respectively defined as
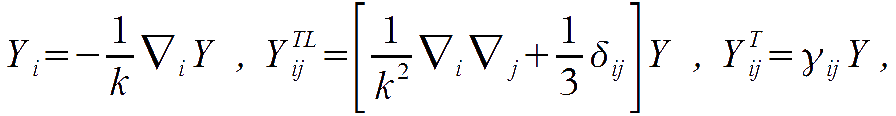
where for tensor we defined the traceless and trace combinations. In flat FRW metric, the eigenfunctions coincide with the plane waves:
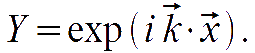
Vector perturbations
The complete system is made of the vector eigenfunctions of the Laplace operator
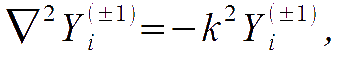
satisfying the divergenceless condition
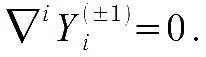
Once again the derivatives of these functions constitute the vector-type component of tensors:
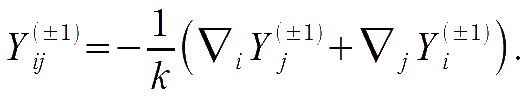
In a flat FRW geometry, a suitable expression is
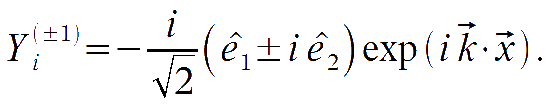
Tensor perturbations
The tensor eigenfunctions of the Laplace operators are
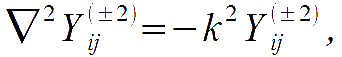
satisfying the transverse traceless conditions
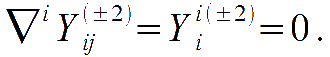
In a flat FRW geometry, a suitable expression is
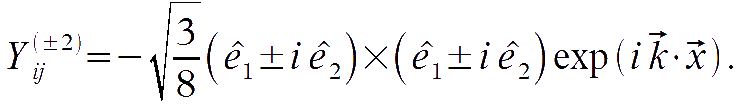
Metric perturbations in the Newtonian gauge
We adopt the Newtonian gauge, where the metric perturbation appear to be isotropic, having only a trace component:
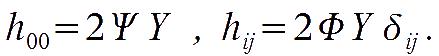
Vectors are specified by
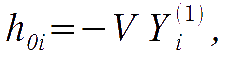
while tensors are gauge invariant:
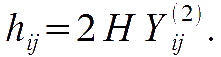
Note that for vectors and tensors we did show just one of the two eigenfunctions; the perturbation relative to the other one has formally the same structure, and we omit it unless otherwise specified.
Stress energy tensor perturbations
Scalar quantities are
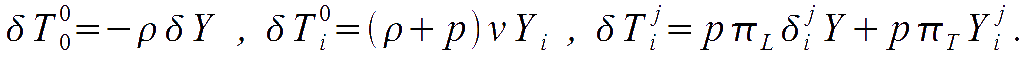
Vector quantities are
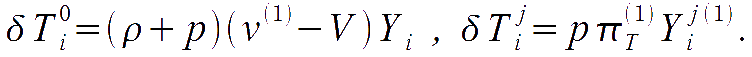
Tensor quantities are
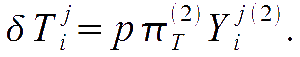
CMB perturbations
Incoming CMB radiation is fully defined by the intensity matrix
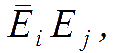
defined by the electric field tensor averaged over a time long compared with the characteristic frequency of the radiation. If the radiation propagation is radial, the intensity matrix lives in the
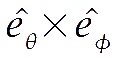
subspace. For CMB black body radiation, the intensity matrix is conveniently defined in terms of the fluctuations from the unperturbed radiation at temperature T. Since it is a tensor living on a two dimensional space, it can be expanded into the Pauli matrices as
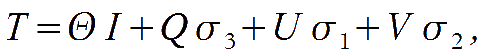
where
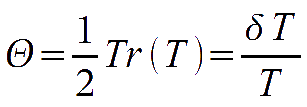
is chosen to be the thermodynamic temperature fluctuation. With this definition,
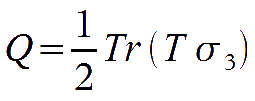
is just the difference in temperature fluctuation for the radiation polarised in the h and v directions. In the same way it can be verified that
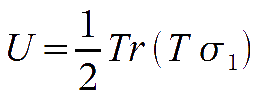
is the same quantity where the axes have been rotated by 45 degrees and
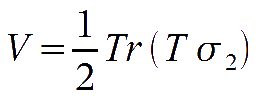
that among the axes
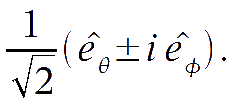
Therefore, Q and U represent the fluctuation for linearly polarised light while V represents circularly polarised radiation. Under rotations in the (h,v) plane, Q and U go one into the other, while V remains distinct. By applying the rotation relations to the Pauli matrices, it can be verified that under rotation by an angle y the following relation hold:
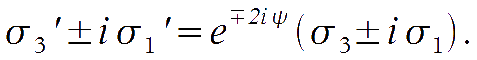
Therefore it is also convenient to recast the T matrix into the form
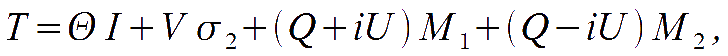
where
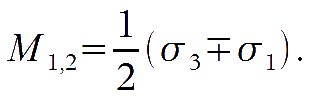
The CMB relevant interactions are with the gravitational metric tensor and with free charged particles, via Thomson scattering. The latter does not generate circularly polarised perturbations, therefore we ignore V from now on. The intensity matrix T is then specified by three numbers:
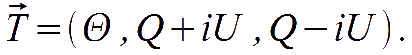
Normal modes
CMB perturbations depend on the conformal time, the space position, as well as the propagation direction:
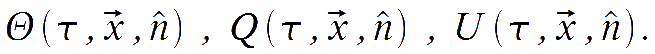
Let us now find a suitable expansion set in the Fourier and harmonic space. Let us consider the temperature first. The expansion in normal modes is made first in the Fourier space:
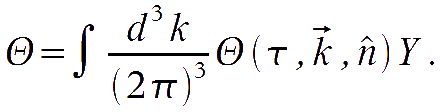
Then, it is necessary to expand the angular dependence. For each Fourier mode, let us define a k-frame where
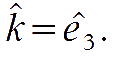
That is convenient for reasons that will be clear below. Let us expand the dependence on the radiation propagation direction in the k-frame, defined as
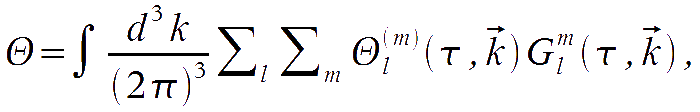
where
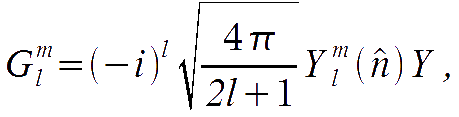
and Y reduces to the plane waves in a flat FRW geometry. Similarly, the expansion of the polarisation quantities can be suitably defined as
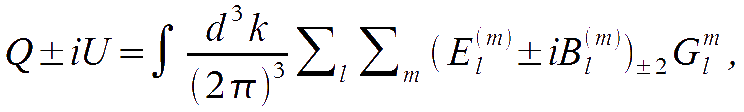
where
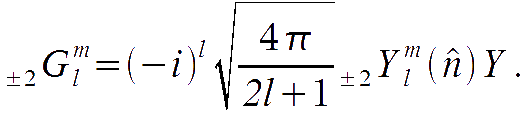
This expansion is convenient because the cosmological perturbations, in the k-frame, excite only modes up to the quadrupole in m. Indeed, it can be verified that the following proportionality relations hold:
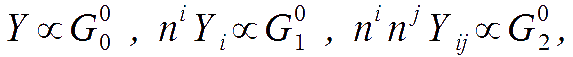
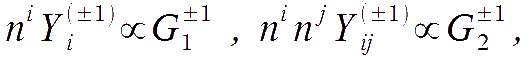
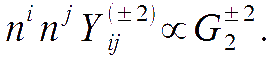
Thus, cosmological perturbations excite only up to the quadrupole in m.
Boltzmann equation
We now turn to derive a Boltzmann equation describing the evolution of the quantities above. It will have a form
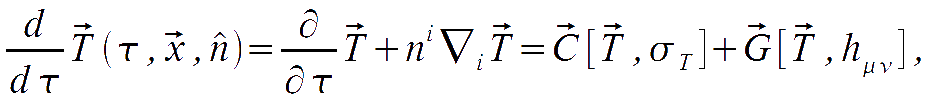
where we used
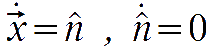
and the last relation holds in a flat FRW metric.
Thomson scattering
Let us consider the radiation scattered by an electron moving under the effect of electromagnetic radiation. Let us define as the scattering plane the one formed by the incoming and outcoming propagation directions, indicated respectively as
![]() or
or
Since the Thomson scattering differential cross section is proportional to
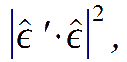
the radiation polarised perpendicularly to the scattering plane is isotropically intense, while the one polarised on the scattering plane gets a factor cos 2 b where b is the scattering angle. Summarizing, in this frame the CMB perturbations get the following transformation rules for Thomson scattering:
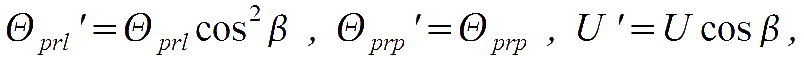
where prl and prp mean parallel and perpendicular polarisation direction with respect to the scattering plane and the transformation for U descends from the one for Q. Note also that
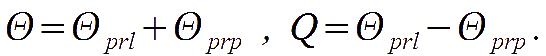
We want to express these scattering relations in the k-frame. For doing so, two steps are necessary: first, rotate the k-frame in such a way that its meridian plane coincides with the plane orthogonal to the direction (h',v'); after scattering, perform a rotation in such a way that the plane orthogonal to (h,v) coincides with the plane orthogonal to the wavevector. After that, the remaining step is to integrate over all the possible incoming directions. The result is
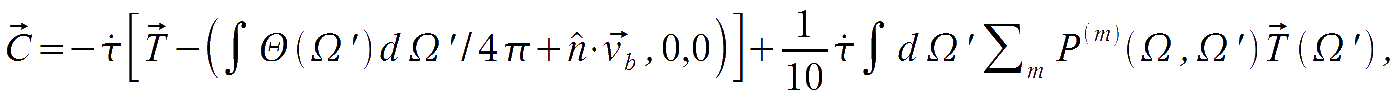
where vb represent the Doppler shift due to the local peculiar velocity of baryons; the matrix P is given by
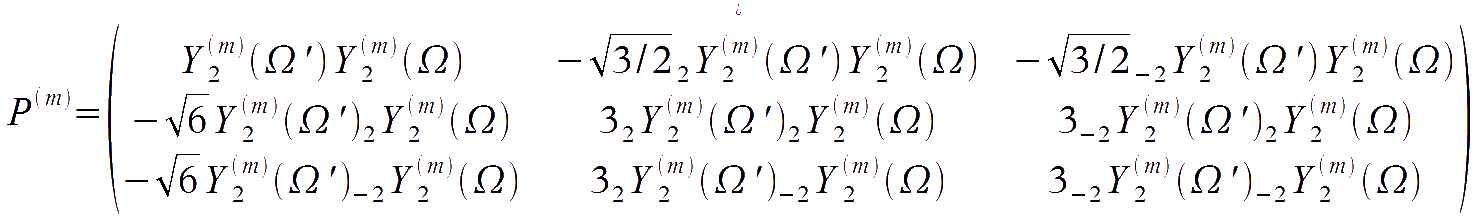
highlighting that the Thomson scattering gets activated by the quadrupole in the temperature anisotropies, and
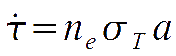
is the collosion rate as a function of the free electron number density, the Thomson scattering cross section, the cosmological scale factor, respectively.
Gravitational scattering
The energy of a photon as seen by an observer having quadri-velocity ul is p=-ulpl , where pl is the photon quadri-momentum. It is possible to demonstrate that the energy redshift for propagation in a perturbed FRW metric is given by
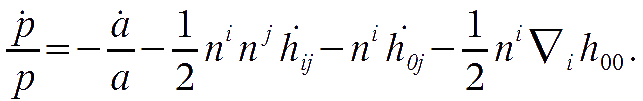
Therefore, the gravitational shift term is given by
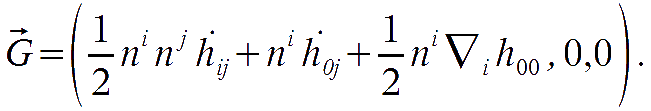
CMB perturbations evolution
Here we obtain the equation for the evolution of CMB perturbations. It is enough to substitute the expansion for the the temperature and polarisation perturbations into the Boltzmann equation derived above and relate the corresponding multipoles:
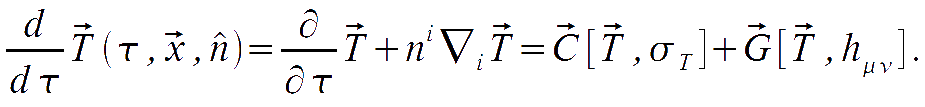
In the Fourier space, the second term in the right hand side becomes
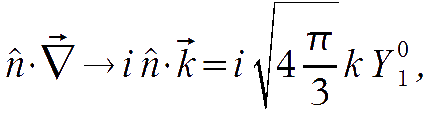
and therefore it multiplies scalar and tensor spherical harmonics into the T term. It is then possible to use the Clebsch-Gordan relation
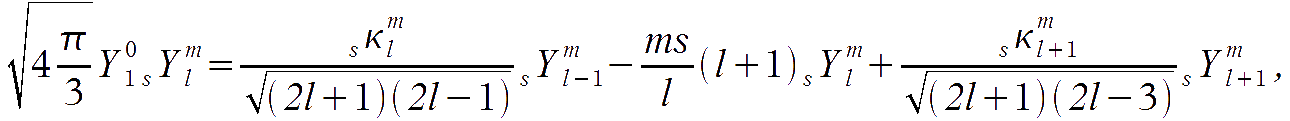
which relates the amplitude in l with l+1 and l-1 terms, and
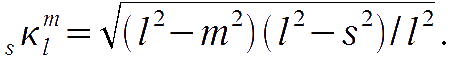
By putting these expression into the Boltzmann equation and substituting the terms in the right hand side as derived above, one obtains
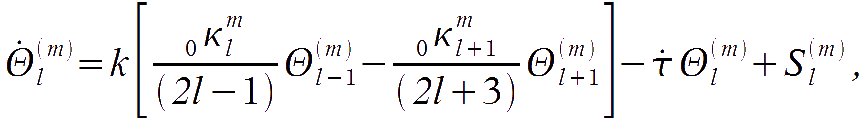
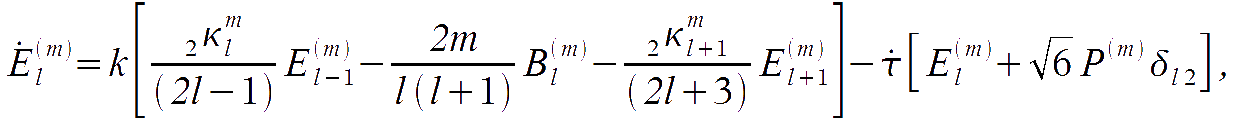
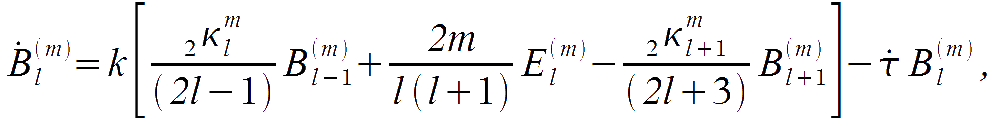
where