


Next: 9 Documentation
Up: User's Guide for the
Previous: 7 Examples, examples_qe, inputs,
Contents
In this section we briefly summarize the color codes of some of the figures
that can be obtained from thermo_pw.
- Total energy versus kinetic energy. This is a single figure of the total
energy versus wave-functions kinetic energy cut-offs. When the test
requires several charge density cut-offs there is a different curve
for each charge density cut-off. The curve corresponding to the lowest
charge density cut-off is red, the one corresponding to the
highest is blue, all the others are green.
Note that the total energy of the last configuration (highest wave function
and charge density cut offs) is subtracted from all energies.
- Total energy versus size of the k-point mesh. This is a single
figure of the total energy as a function of the size of the k-point
mesh. When the test requires several values of degauss, there
is a curve for each degauss. The curve corresponding to the
first degauss is red, the one corresponding to the
last is blue, all the others are green.
Note that the total energy of the last configuration (highest number of
points and lowest degauss) is subtracted from all energies.
- Total energy as a function of volume (lmurn=.TRUE.).
This plot is composed of two figures. Total energy as a function of volume
and pressure as a function of volume. Both curves are red.
The points on the first curve are the energies calculated by
pw.x, the continuous curve is the fit.
- Total energy as a function of one or two crystallographic parameters
(lmurn=.FALSE.). When there is a single parameter the curve is
red as in the case lmurn=.TRUE.. When there are two
parameters a contour plot of the energy as a function of two parameters
is shown. The contour levels, their number and their colors can be
given in input. By default the code shows nine levels with three
colors. From the lowest to the highest levels, the colors are red,
green, and blue. The energy value of each level is
written on output. When the user requests more levels without specifying
their colors, the code continues with three yellow levels,
then pink, cyan, orange, black, and
when more than 24
levels are requested the sequence of colors is repeated.
For orthorhombic solids the code produces many postscript figures, one
for each value of c/a
on the grid. In each figure there is a contour
plot of the energy as a function of a
and b/a
. The colors of the levels
follow the same conventions of the previous case. When the levels are chosen
by the code the entire energy range (for all c/a
) is divided into nine
levels so each figure might have less that nine curves.
For crystal systems with more crystallographic parameters, this figure is
not available.
- Energy bands. In this figure the bands have the color of
their irreducible representation. Each line of the path can have a different
point group and set of representations. See the point_groups.pdf file
for the list of representations and their color code.
When the symmetry analysis is not done all the bands are red.
- Energy bands with enhance_plot=.TRUE.. In this case
the background color of the panels with lines at the zone border are
gray, yellow, or pink. Gray means that the point group (or double point
group) representations are used, yellow or pink means that a gauge
transformation was applied and projective representations might have been used.
A yellow background indicates that no switch
from the point group to the double point group or viceversa was made,
while a pink background means that such a switch was necessary.
- Electron density of states. This is a plot composed of two figures,
the first contains the electron density of states, the second the integral
of the density of states up to that energy. The dos is red.
In the local spin density case, the dos for spin up is red the
one for spin down is blue and with a negative sign.
The integrated density of states is blue. In the spin polarized
case, the curve shows the integral of the sum of the up and down density
of states.
- Electronic energy, free energy, entropy, and isochoric heat capacity
(metals only). This plot is composed of four pictures one for each
quantity. There is a single blue curve per plot.
- Dielectric constant as a function of frequency (
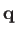 =
= 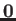 ). There are
two plots, one for the real part and one for the imaginary part.
Other two plots contain the real and imaginary part of the complex index
of refraction. For cubic solids other two plots show the reflectivity
for normal incidence and the absorption coefficient.
All curves are in red. For hexagonal, trigonal, and tetragonal
systems the xx
component is in red, while the zz
component is in green.
For orthorombic systems the xx
component is in red, the yy
component in
green and the zz
component in blue. For monoclinic and triclinic
systems the plot is not done.
). There are
two plots, one for the real part and one for the imaginary part.
Other two plots contain the real and imaginary part of the complex index
of refraction. For cubic solids other two plots show the reflectivity
for normal incidence and the absorption coefficient.
All curves are in red. For hexagonal, trigonal, and tetragonal
systems the xx
component is in red, while the zz
component is in green.
For orthorombic systems the xx
component is in red, the yy
component in
green and the zz
component in blue. For monoclinic and triclinic
systems the plot is not done.
- Inverse of the dielectric constant as a function of frequency
(
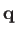
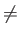
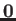 ). There are four plots: the real and imaginary part of
). There are four plots: the real and imaginary part of
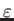 (
(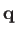 ,
,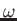 )
and the real and imaginary part of
1/
)
and the real and imaginary part of
1/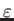 (
(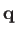 ,
,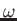 )
. They are all in red. Note that the latter
is really calculated, while the first is just its inverse.
)
. They are all in red. Note that the latter
is really calculated, while the first is just its inverse.
- Phonon dispersions. In this figure the phonon dispersions have the color
of their irreducible representations. The same comments made for the plot of
the band structure apply here.
- Phonon dos. There is one picture with a single red curve.
- Vibrational energy, free energy, entropy, and isochoric heat capacity. This plot
is composed of four figures each one showing one quantity. In red the
quantities obtained using the phonon density of states,
in blue those obtained from integration over
the Brillouin zone. In some cases the red curve is not visible
because it is exactly below the blue one.
- Atomic B factors as a function of temperature. This plot is composed of
one figure for each atom for cubic solids and of two figures for each atom
in the other cases. One figure contains Bxx
(red, pink), Byy
(blue, light_blue) and Bzz
(dark_green, green) as a function of
temperature. The first color refers to quantities calculated from
generalized phonon density of states while the second refers to quantities
calculated by Brillouin zone integration.
If the curves coincide, only the last one (green) will be visible. The second
figure, when plotted shows Bxy
(red, pink), Bxz
(blue, light_blue),
and Byz
(dark_green, green).
- Debye vibrational energy, free energy,
entropy, and isochoric heat capacity. This plot is composed of four
figures, one for each quantity. The curves are in blue
and the word Debye appears in the y
axis label.
- Equilibrium volume, Helmholtz (or Gibbs at finite pressure) free energy,
bulk modulus, pressure derivative of the bulk
modulus, volume thermal expansion, isochoric heat capacity,
isobaric heat capacity, isobaric-isochoric difference of the heat capacity,
isoentropic-isothermal difference of the bulk modulus, and
average Grüneisen parameter as a function of temperature
(lmurn=.TRUE.).
This plot is composed of ten figures, one for each
quantity in the order given above. The quantities
calculated using the phonon dos are in red, those
obtained by an integral over the Brillouin zone are in blue.
The volume thermal expansion can be calculated using the mode Grüneisen
parameters and is plotted in green.
The isobaric-isochoric difference of the heat capacity, the
isoentropic-isothermal difference of the bulk modulus, and
average Grüneisen parameter calculated with this volume thermal expansion
are plotted in green. The volume and the bulk modulus used to
compute the volume thermal expansion via the mode Grüneisen parameters
are the blue ones if ltherm_freq=.TRUE.
or the red ones if ltherm_freq=.FALSE. and
ltherm_dos=.TRUE..
When both ltherm_freq=.FALSE. and ltherm_
dos=.FALSE.
the equilibrium values of the volume and of the bulk modulus calculated
at T = 0
K are used at all temperatures.
The equilibrium volume at T = 0
K is used at all temperatures also when
lv0_t=.FALSE..
The equilibrium bulk modulus at T = 0
K is used all temperatures also
when lb0_t=.FALSE.
- Crystallographic parameters, volume, Helmholtz (or Gibbs at finite pressure)
free energy, thermal expansion tensor, volume thermal expansion, constant
strain heat capacity (
C
 ), isobaric heat capacity (CP
),
difference CP - CV
of isobaric and isochoric heat capacities,
difference
C
), isobaric heat capacity (CP
),
difference CP - CV
of isobaric and isochoric heat capacities,
difference
C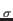 - C
- C of constant stress and
constant strain heat capacities (note that
C
of constant stress and
constant strain heat capacities (note that
C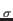 = CP
),
difference
CV - C
= CP
),
difference
CV - C of isochoric and constant strain heat capacities,
difference BS - BT
of the isoentropic and isothermal bulk modulus,
and average Grüneisen parameter as a function of temperature
(lmurn=.FALSE.). The number of
figures in this plot depends on the crystal system and on the presence
of one or more files with the elastic constants. It shows a
as a function
of temperature for cubic solids, a
, c/a
, and c
for tetragonal and
hexagonal
solids. For orthorhombic solids it shows also b/a
and b
while for
trigonal solids
it shows a
and
cos
of isochoric and constant strain heat capacities,
difference BS - BT
of the isoentropic and isothermal bulk modulus,
and average Grüneisen parameter as a function of temperature
(lmurn=.FALSE.). The number of
figures in this plot depends on the crystal system and on the presence
of one or more files with the elastic constants. It shows a
as a function
of temperature for cubic solids, a
, c/a
, and c
for tetragonal and
hexagonal
solids. For orthorhombic solids it shows also b/a
and b
while for
trigonal solids
it shows a
and
cos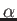 . For monoclinic
solids it shows a
, b/a
, b
, c/a
, c
, and
cos
. For monoclinic
solids it shows a
, b/a
, b
, c/a
, c
, and
cos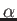 (c-unique) or
cos
(c-unique) or
cos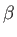 (b-unique). All the six crystallographic parameters
as a function of temperature are shown for triclinic solids.
All quantities calculated using the phonon
density of states are in red, those calculated integrating
over the Brillouin zone are in blue with the exception of the
thermal expansion tensor. When this tensor is diagonal with all identical
components it follows the above rules while the tensor computed
from mode Grüneisen parameters is in green. For hexagonal,
tetragonal and trigonal solids
(b-unique). All the six crystallographic parameters
as a function of temperature are shown for triclinic solids.
All quantities calculated using the phonon
density of states are in red, those calculated integrating
over the Brillouin zone are in blue with the exception of the
thermal expansion tensor. When this tensor is diagonal with all identical
components it follows the above rules while the tensor computed
from mode Grüneisen parameters is in green. For hexagonal,
tetragonal and trigonal solids
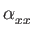 follows the above rules
while
follows the above rules
while
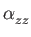 is pink, cyan, and orange
when computed from phonon density of states, Brillouin zone integration,
or mode Grüneisen parameters, respectively.
In the orthorhombic case
is pink, cyan, and orange
when computed from phonon density of states, Brillouin zone integration,
or mode Grüneisen parameters, respectively.
In the orthorhombic case
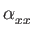 and
and
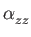 have the same
colors, while
have the same
colors, while
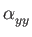 is gold, olive, and
light-blue in the three cases, respectively. For the other
crystal systems the thermal expansion tensor is not given.
The thermal expansion tensor from the mode Grüneisen parameters is
calculated only when the elastic_constants directory contains at
least one file with the elastic constants. In this case also
CP - CV
,
C
is gold, olive, and
light-blue in the three cases, respectively. For the other
crystal systems the thermal expansion tensor is not given.
The thermal expansion tensor from the mode Grüneisen parameters is
calculated only when the elastic_constants directory contains at
least one file with the elastic constants. In this case also
CP - CV
,
C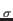 - C
- C ,
CV - C
,
CV - C , and the
average Grüneisen parameters are calculated using this thermal
expansion tensor and plotted in green.
The volume used in these calculations is the blue curve
if ltherm_freq=.TRUE.
or as in the red curve if ltherm_freq=.FALSE.
and ltherm_dos=.TRUE..
When both ltherm_freq=.FALSE. and ltherm_dos=.FALSE.
the volume is kept fixed at the equilibrium volume at T = 0
K.
The same applies for the bulk modulus calculated from a single elastic
constant file when the flag lb0_t=.FALSE. or computed
within the ``quasi-static'' approximation when lb0_t=.TRUE..
The CP
,
C
, and the
average Grüneisen parameters are calculated using this thermal
expansion tensor and plotted in green.
The volume used in these calculations is the blue curve
if ltherm_freq=.TRUE.
or as in the red curve if ltherm_freq=.FALSE.
and ltherm_dos=.TRUE..
When both ltherm_freq=.FALSE. and ltherm_dos=.FALSE.
the volume is kept fixed at the equilibrium volume at T = 0
K.
The same applies for the bulk modulus calculated from a single elastic
constant file when the flag lb0_t=.FALSE. or computed
within the ``quasi-static'' approximation when lb0_t=.TRUE..
The CP
,
C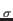 - C
- C ,
CV - C
,
CV - C , and
the average Grüneisen parameter are plotted only in presence of
one or more elastic constants file.
, and
the average Grüneisen parameter are plotted only in presence of
one or more elastic constants file.
- Thermal stresses as a function of temperature. This plot is composed of
one figure in cubic solids and of two figures in the other cases.
One figure contains bxx
(red, pink), byy
(blue, light_blue)
and bzz
(dark_green, green) as a function of temperature.
The first color refers to quantities calculated from phonon density of states
while the second refers to quantities calculated by Brillouin zone
integration. If the curves coincide, only the last one (green) will
be visible. The second figure, when plotted, shows bxy
(red, pink),
bxz
(blue, light_blue), and byz
(dark_green, green).
- Mode Grüneisen parameters. In this plot the mode Grüneisen parameters have
the color of the irreducible representation of the phonon dispersion curve
of which they are the derivative.
The same comments made for the band structure plot apply here.
- Generalized average Grüneisen parameters as a function of temperature.
This plot is composed of one figure in cubic solids and of two figures in
the other cases.
One figure contains
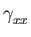 (red, pink),
(red, pink),
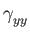 (blue, light_blue)
and
(blue, light_blue)
and
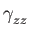 (dark_green, green) as a function of temperature.
The first color refers to quantities calculated from phonon density of states
while the second color refers to quantities calculated by Brillouin zone
integration.
If the curves coincide, only the last one (green) will be visible.
The second figure,
when plotted shows
(dark_green, green) as a function of temperature.
The first color refers to quantities calculated from phonon density of states
while the second color refers to quantities calculated by Brillouin zone
integration.
If the curves coincide, only the last one (green) will be visible.
The second figure,
when plotted shows
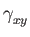 (red, pink),
(red, pink),
 (blue, light_blue), and
(blue, light_blue), and
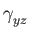 (dark_green, green).
(dark_green, green).
- Phonon dispersions at the geometry that corresponds to a given temperature.
The colors are assigned on the basis of the irreducible representation of
each mode. The same comments made for the band structure plot apply here.
- Temperature dependence of the isothermal and isoentropic elastic constants
within the `Quasi-static', `Fixed geometry quasi-harmonic' or
'Quasi-harmonic approximation'. There is a plot for each non-zero
elastic constant and a plot of the bulk modulus. The number of plots
depends on the Laue class.
Elastic constants
interpolated at the geometry computed using the phonon density of states
are in red (isothermal) and green (isoentropic),
those calculated from integration over the
Brillouin zone are in blue (isothermal) and orange
(isoentropic).
- Temperature dependence of the isothermal and isoentropic elastic compliances
within the `Quasi-static', `Fixed geometry quasi-harmonic' or
'Quasi-harmonic approximation'. There is a plot for each non-zero
elastic compliance and a plot of the compressibility. The number of plots
depends on the Laue class.
Elastic compliances
interpolated at the geometry computed using the phonon density of states
are in red (isothermal) and green (isoentropic),
those calculated from integration over the
Brillouin zone are in blue (isothermal) and orange
(isoentropic).
- Temperature dependence of the isothermal elastic constants within the
`Fixed geometry quasi-harmonic approximation' for all the geometries of
the mesh. There is a plot for each non-zero
elastic constant and a plot of the bulk modulus. The number of plots
depends on the Laue class.
Elastic constants of the different geometries are in the sequence
red, green, blue, yellow,
pink, cyan, orange, black. When there
are more than eight geometries the sequence is repeated.
The same colors are used for the elastic constants obtained with the
phonon density of states or from the integration over the Brillouin zone.
- Temperature dependence of the isothermal elastic compliances within the
`Fixed geometry quasi-harmonic approximation' for all the geometries of
the mesh. There is a plot for each non-zero
elastic compliance and a plot of the compressibility. The number of plots
depends on the Laue class.
Elastic compliances of the different geometries are in the sequence
red, green, blue, yellow,
pink, cyan, orange, black. When there
are more than eight geometries the sequence is repeated.
The same colors are used for the elastic compliances obtained with the
phonon density of states or from the integration over the Brillouin zone.



Next: 9 Documentation
Up: User's Guide for the
Previous: 7 Examples, examples_qe, inputs,
Contents
2021-07-20