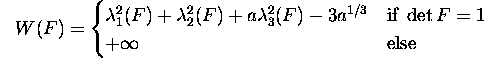
Nematic Elastomers: BTW Energy |
The experimentally observed material instabilities can be studied through energy minimization (Bladon, Terentjev, and Warner 1993, Weilepp and Brand 1996, Verwey et al. 1996, Warner and Terentjev 1996, Finkelmann et al. 1997). In particular, the expression for the free energy density proposed by Bladon, Terentjev, and Warner is
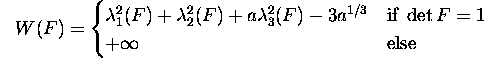
This energy has no intrinsic length scale, hence it is unable to establish a finite size for the oscillations of the nematic director.
The quasiconvex envelope
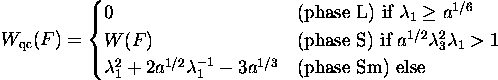
shows the appearance of three different phases. The corresponding phase diagram is shown in the Figure.
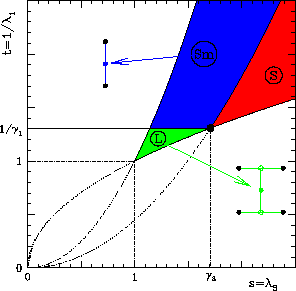
All deformations in the liquid phase L can be decomposed in four zero-energy gradients (laminates within laminates). The resulting effective energy is flat, hence the response of the material is liquid-like.
For macroscopic deformations in phase S one of the principal strains is large, and the director is naturally parallel to the associated eigenvector. Hence the freedom to form microstructure does not permit to reduce the energy, and the mechanical response is that of a solid rubber.
Deformations in the ``smectic'' region Sm are
characterized by one small singular value,
with the two other singular values close to each other.
The effective energy is determined by the smallest principal stretch
alone, and the response of the material is solid-like along the
corresponding eigenvector, and liquid-like in the orthogonal plane.
These deformations correspond to oscillatory patterns with two
alternating shears (simple laminates), with nonzero transmitted
stresses.
Forward:
Experiments and geometry