



Next: Programma: newton
Up: Moto di un punto
Previous: Moto di un punto
Contents
La strategia generale per integrare la (1.1)
è quella di suddividere l'intervallo
temporale di interesse ![$[0,T]$](img7.gif) in
in 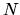 intervallini di
ampiezza
intervallini di
ampiezza 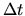 , sufficientemente piccoli da non
commettere grossi errori approssimando la soluzione
, sufficientemente piccoli da non
commettere grossi errori approssimando la soluzione
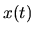 con il suo sviluppo in serie di Taylor fino ad
un ordine relativamente basso, e integrare una
equazione alle differenze finite per ottenere
con il suo sviluppo in serie di Taylor fino ad
un ordine relativamente basso, e integrare una
equazione alle differenze finite per ottenere
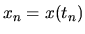 , dove
, dove
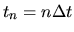 ,
, 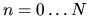 .
.
Espandendo in serie di Taylor attorno a 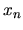 in
entrambe le direzioni:
in
entrambe le direzioni:
![\begin{displaymath}
\begin{array}{l}
x_{n-1} = x_n - \dot{x}_n \Delta t + (1/2) ...
.../6) \dot{\ddot{x}}_n (\Delta t)^3 + O[(\Delta t)^4]
\end{array}\end{displaymath}](img14.gif) |
(1.2) |
e sommandole fra loro si ottiene
![\begin{displaymath}
x_{n+1} = 2x_n - x_{n-1} + \ddot{x}_n (\Delta t)^2 + O[(\Delta t)^4]
\end{displaymath}](img15.gif) |
(1.3) |
Ora utilizziamo la legge di Newton (1.1), o
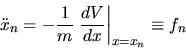 |
(1.4) |
ottenendo
![\begin{displaymath}
x_{n+1} = 2x_n - x_{n-1} + f_n (\Delta t)^2 + O[(\Delta t)^4] .
\end{displaymath}](img17.gif) |
(1.5) |
Questa equazione ci permette, nota la posizione ai tempi
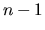 e
e 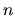 e la forza al tempo
e la forza al tempo 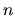 , di ottenere una stima
della posizione al tempo
, di ottenere una stima
della posizione al tempo 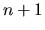 , e quindi fornisce un algoritmo
(detto algoritmo di Størmer-Verlet) per ottenere
iterativamente la traiettoria
, e quindi fornisce un algoritmo
(detto algoritmo di Størmer-Verlet) per ottenere
iterativamente la traiettoria 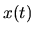 del punto sotto
forma di una tabella numerica.
del punto sotto
forma di una tabella numerica.




Next: Programma: newton
Up: Moto di un punto
Previous: Moto di un punto
Contents
furio
2002-02-24
![]() in
in ![]() intervallini di
ampiezza
intervallini di
ampiezza ![]() , sufficientemente piccoli da non
commettere grossi errori approssimando la soluzione
, sufficientemente piccoli da non
commettere grossi errori approssimando la soluzione
![]() con il suo sviluppo in serie di Taylor fino ad
un ordine relativamente basso, e integrare una
equazione alle differenze finite per ottenere
con il suo sviluppo in serie di Taylor fino ad
un ordine relativamente basso, e integrare una
equazione alle differenze finite per ottenere
![]() , dove
, dove
![]() ,
, ![]() .
.
![]() in
entrambe le direzioni:
in
entrambe le direzioni: