Degenerazione accidentale e simmetria dinamica

Nonostante il potenziale efficace che appare nella (4.31) dipenda da $\ell$, e la parte angolare delle autofunzioni pure dipenda assai fortemente da $\ell$, l'espressione (4.36) dipende solo da $n$. Abbiamo dunque una degenerazione delle energie sugli $n$ possibili valori per $\ell$, che si aggiunge a quella di ordine $2\ell+1$ legata ai possibili valori del numero quantico $m$ [implicata dalla (4.17) in cui $m$ non appare]. La degenerazione complessiva^4.1 associata a $n$ è

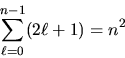$$\sum_{\ell=0}^{n-1} (2\ell+1) = n^2$$ (4.44)

La degenerazione delle energie per diversi valori di $\ell$ è una situazione molto particolare che si verifica soltanto quando il potenziale di interazione è coulombiano. Si tratta di cioè di una degenerazione accidentale, che scompare appena il potenziale non è più puramente coulombiano.

Una degenerazione indica generalmente la presenza di una simmetria, e quindi di una quantità conservata. Ad esempio la degenerazione in $m$ è legata alla simmetria sferica e alla conservazione del momento angolare. Si può far vedere che il corrispondente classico della degenerazione accidentale negli atomi idrogenoidi è la conservazione del vettore di Runge-Lenz

$${\bf M} = \frac{ {\bf p} \times {\bf L} }{m} -\frac{k}{r} {\bf r}$$ (4.45)

verificata per una hamiltoniana classica

$$H = \frac{p^2}{2m} - \frac{k}{r}$$ (4.46)

È questo il caso del moto relativo di due corpi attratti dalla forza gravitazionale. Come ben noto, le orbite sono ellittiche, e sono orbite chiuse: l'orientazione dell'ellisse non cambia nel tempo. Il vettore di Runge-Lenz è diretto lungo l'asse maggiore dell'ellisse.

Il corrispondente vettore quantistico ha una espressione lievemente diversa ma sostanzialmente simile:

$${\bf M} = \frac{1}{2m} \left( {\bf p} \times {\bf L} - {\bf L} \times {\bf p} \right) - \frac{2Z}{r}$$ (4.47)

e si può far vedere che ${\bf M}$ è ortogonale a ${\bf L}$, e $[{\bf M},H]=0$: ossia è una quantità conservata.