



Next: Laboratorio
Up: Metodi approssimati
Previous: Sviluppo in funzioni non
Contents
Il programma
hydrogen_gauss
risolve il problema secolare per l'atomo di idrogeno
utilizzando due diverse basi non ortonormali:
- una base gaussiana ``onda S'':
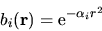 |
(5.91) |
- una base gaussiana ``onda P'':
L'operatore hamiltoniano del problema è ovviamente
(in unità atomiche con energie date in Rydberg)
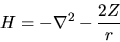 |
(5.95) |
e per l'atomo di idrogeno 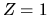 .
.
Il programma permette di assegnare gli esponenti 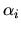 ,
sotto forma di larghezze
,
sotto forma di larghezze 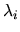 delle gaussiane:
delle gaussiane:
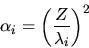 |
(5.96) |
Gli esponenti vengono fatti corrispondere a una griglia di
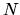 valori di
valori di 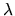 equispaziati da un minimo ad un
massimo specificati.
I calcoli per l'onda S e l'onda P sono del tutto indipendenti:
si tratta di due basi distinte. La base in onda P è
chiaramente inadatta a descrivere lo stato fondamentale,
perchè non è possibile riprodurre il giusto andamento
per piccoli
equispaziati da un minimo ad un
massimo specificati.
I calcoli per l'onda S e l'onda P sono del tutto indipendenti:
si tratta di due basi distinte. La base in onda P è
chiaramente inadatta a descrivere lo stato fondamentale,
perchè non è possibile riprodurre il giusto andamento
per piccoli 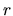 , e viene inclusa a scopo didattico.
, e viene inclusa a scopo didattico.
Il codice procede quindi a valutare tutti gli elementi
delle matrici 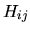 e
e 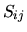 . Il calcolo è basato
sulle espressioni degli integrali calcolati analiticamente.
In particolare si trova per l'onda S
. Il calcolo è basato
sulle espressioni degli integrali calcolati analiticamente.
In particolare si trova per l'onda S
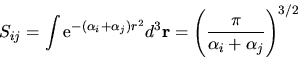 |
(5.97) |
e inoltre i termini cinetico e coulombiano di 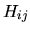 sono rispettivamente
sono rispettivamente
![\begin{displaymath}
H^K_{ij} = \int {\rm e}^{-\alpha_i r^2} [-\nabla^2]
{\rm e}^...
..._i+\alpha_j}
\left(\frac{\pi}{\alpha_i+\alpha_j}\right)^{3/2}
\end{displaymath}](img846.gif) |
(5.98) |
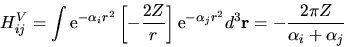 |
(5.99) |
Per l'onda P si procede analogamente, utilizzando le corrispondenti
espressioni per gli integrali.
Il codice procede dunque a chiamare la subroutine diaghg
che risolve il problema secolare generalizzato (ossia
applica il principio variazionale), ritornando il vettore
e contenente gli autovalori in ordine crescente di energia,
e la matrice v contenente gli autovettori, ossia i
coefficienti dell'espansione.
Al suo interno, diaghg effettua il calcolo in due stadi
descritto nella sezione precedente, delegando la risoluzione
del problema agli autovalori semplice alla subroutine
dsyev della libreria di algebra lineare
LAPACK,
ed utilizzando alcune chiamate addizionali a subroutines della libreria
BLAS.
Informazioni addizionali su queste librerie sono disponibili a
partire dalla pagina del corso
lapack.html.
Da notare che dopo la prima diagonalizzazione (relativa
a 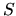 ) diaghg getta via tutti gli autovettori corrispondenti
ad autovalori nulli (entro una soglia di tolleranza numerica).
Questi corrispondono a combinazioni linearmente dipendenti dalle
altre. Il numero di vettori di base linearmente indipendenti
trovati viene riportato nell'output.
) diaghg getta via tutti gli autovettori corrispondenti
ad autovalori nulli (entro una soglia di tolleranza numerica).
Questi corrispondono a combinazioni linearmente dipendenti dalle
altre. Il numero di vettori di base linearmente indipendenti
trovati viene riportato nell'output.
Il programma procede quindi a scrivere i coefficienti
dell'espansione nel file s-coeff.out (p-coeff.out):
per ogni funzione 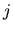 , e la funzione d'onda dello stato
fondamentale nel file s-wfc.out (p-wfc.out).
, e la funzione d'onda dello stato
fondamentale nel file s-wfc.out (p-wfc.out).
Subsections




Next: Laboratorio
Up: Metodi approssimati
Previous: Sviluppo in funzioni non
Contents
furio
2002-02-24
![]() ,
sotto forma di larghezze
,
sotto forma di larghezze ![]() delle gaussiane:
delle gaussiane:
![]() e
e ![]() . Il calcolo è basato
sulle espressioni degli integrali calcolati analiticamente.
In particolare si trova per l'onda S
. Il calcolo è basato
sulle espressioni degli integrali calcolati analiticamente.
In particolare si trova per l'onda S
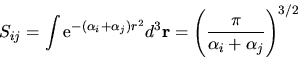
![\begin{displaymath}
H^K_{ij} = \int {\rm e}^{-\alpha_i r^2} [-\nabla^2]
{\rm e}^...
..._i+\alpha_j}
\left(\frac{\pi}{\alpha_i+\alpha_j}\right)^{3/2}
\end{displaymath}](img846.gif)
![]() ) diaghg getta via tutti gli autovettori corrispondenti
ad autovalori nulli (entro una soglia di tolleranza numerica).
Questi corrispondono a combinazioni linearmente dipendenti dalle
altre. Il numero di vettori di base linearmente indipendenti
trovati viene riportato nell'output.
) diaghg getta via tutti gli autovettori corrispondenti
ad autovalori nulli (entro una soglia di tolleranza numerica).
Questi corrispondono a combinazioni linearmente dipendenti dalle
altre. Il numero di vettori di base linearmente indipendenti
trovati viene riportato nell'output.
![]() , e la funzione d'onda dello stato
fondamentale nel file s-wfc.out (p-wfc.out).
, e la funzione d'onda dello stato
fondamentale nel file s-wfc.out (p-wfc.out).