



Next: Bibliography
Up: Ricerca degli zeri
Previous: Metodo di Newton-Raphson
Contents
Metodo della secante
Ci si basa su uno sviluppo lineare di 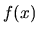 tra due punti
successivi della sequenza di iterazione,
tra due punti
successivi della sequenza di iterazione, 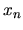 e
e 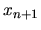 :
:
![\begin{displaymath}
f(x) = f(x_{n-1}) + \frac{x - x_{n-1}}{x_n - x_{n-1}}
\left[ f(x_n) - f(x_{n-1}) \right]
\end{displaymath}](img991.gif) |
(B.3) |
che fornisce come stima per il punto di zero
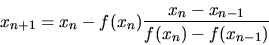 |
(B.4) |
Si procede iterando in questo modo.
Non è necessario che il punto di zero sia contenuto
all'interno dell'intervallo esaminato. A causa di
ciò, è però possibile che in casi patologici
l'algoritmo non converga.
Nei casi regolari, la velocità di convergenza
è comunque assai migliore del metodo di bisezione, anche
se lievemente inferiore a quella del metodo di Newton-Raphson
(che però richiede la conoscenza della derivata).
Nei casi più delicati è conveniente operare la ricerca
in due fasi, iniziando col metodo di bisezione, identificando
lo zero in modo sicuro, e passando infine
al metodo della secante per stabilizzare rapidamente il
valore fino alla precisione richiesta.




Next: Bibliography
Up: Ricerca degli zeri
Previous: Metodo di Newton-Raphson
Contents
furio
2002-02-24
![]() tra due punti
successivi della sequenza di iterazione,
tra due punti
successivi della sequenza di iterazione, ![]() e
e ![]() :
: