Bias Exchange Metadynamics

Bias-exchange metadynamics (see Ref. [1]) is an approach specifically designed for accelerating rare events/computing the free energy in very complex cases, in which the variables that are relevant for the process are more than 2-3. In these cases, normal approaches such as metadynamics or umbrella sampling are very inefficient.
The method works as follows:

• One first lists all the collective variables that are expected to be relevant for the process under investigation. There is no limitation on the number of variables.
• One runs in parallel several molecular dynamics simulations, each biased with a metadynamics potential acting on one of the collective variables of the list.
• At fixed time intervals, swaps of the configurations between pairs of replicas are attempted. The swap is accepted according to the Metropolis criterion.

Thus, the dynamics of each replica is biased in a direction that changes stochastically with time. This allows the system exploring a complex (multidimensional) free energy landscape with great efficiency, even if the bias at each time is only one-dimensional.


A two-dimensional example

Consider a dynamics on a two-dimensional potential like the one in figure. If one perfoms metadynamics biasing x, one obtains an estimate of the free energy affected by large errors: indeed, the system jumps between the two wells at the bottom and the two wells at the top only due to (rare) thermal fluctuations, and obtaining the correct free energy would require taking the average over several transitions along y.



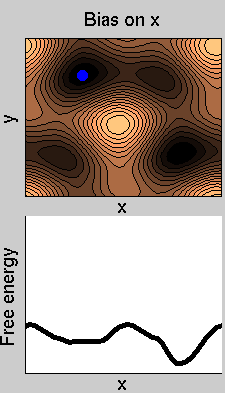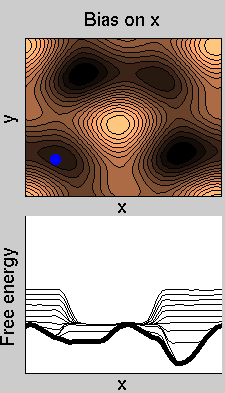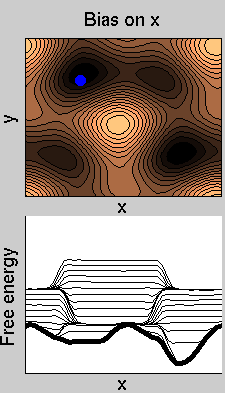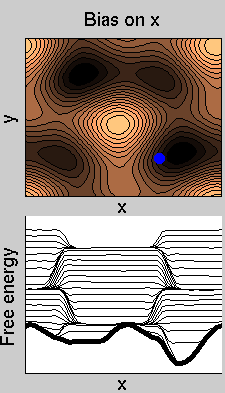
We now perform two metadynamics simulations on two replicas, one biasing x, the other y. From time to time, we allow the two replicas exchanging configurations, accepting the exchange according to a Metropolis criterion (see Ref. [1]). Even if the computational cost has only dubled with respect to the simulation above, one observes a very significant reduction of the hysteresis:


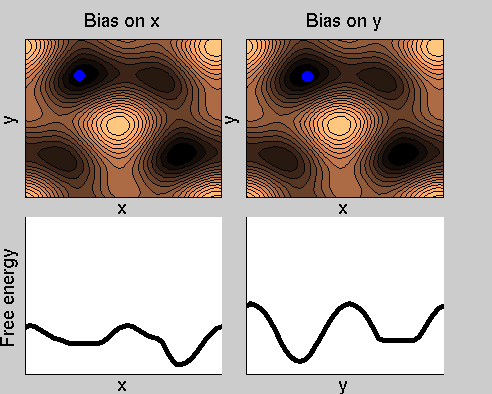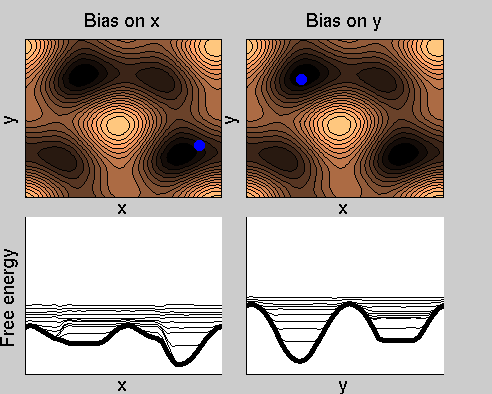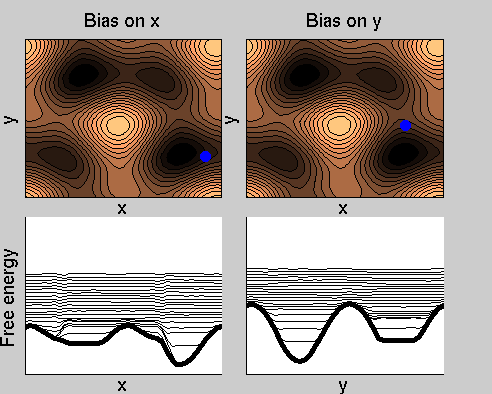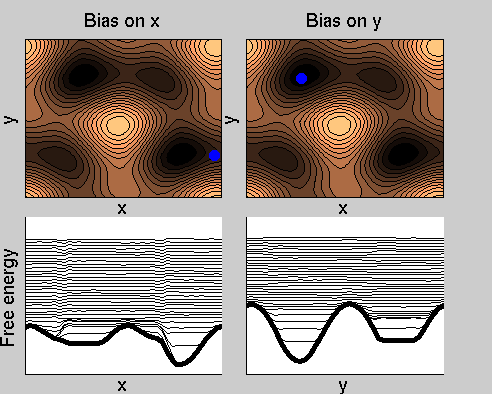
Now the metadynamics potential almost exactly compensates the free energy, both as a function of x and y: indeed, the profiles are practically flat lines. This means that the hysteresis is much reduced, and the metadynamics potential provides a very good estimate of the free energy.

• The approach allows a parallel reconstruction of the free energy as a function of many variables. The computational cost scales LINEARLY with the number of variables.
• The more variables one adds, the better the convergence is. However, if one forgets a relevant variable convergence is slow.
• If one uses NR variable, the result of the simulation is not a free energy as a function of NR variables, but NR one-dimensional projections of the free energy. Obtaining the free energy as a function of all the variables requires a postprocessing of the results, described in Ref. [2].

The method has been successfully applied to study protein folding and protein-ligand docking.
Bibliography
[1] S Piana, A Laio,
A bias-exchange approach to protein folding
JOURNAL OF PHYSICAL CHEMISTRY B, 111, 4553 (2007)

[2] F Marinelli, F Pietrucci, A Laio, S Piana,
A Kinetic Model of Trp-Cage Folding from Multiple Biased Molecular Dynamics Simulations
PLOS COMPUTATIONAL BIOLOGY, 5, e1000452 (2009)