



Next: L'algoritmo di Størmer-Verlet
Up: Una applicazione classica
Previous: Una applicazione classica
Contents
Moto di un punto materiale
Vogliamo ottenere la legge del moto di
un punto materiale di massa 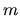 in una dimensione,
soggetto ad un potenziale
in una dimensione,
soggetto ad un potenziale 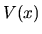 .
.
L'equazione differenziale che governa il moto del punto
(ossia fornisce 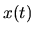 )
date la posizione e la velocità iniziali, è la seconda
legge di Newton
)
date la posizione e la velocità iniziali, è la seconda
legge di Newton
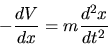 |
(1.1) |
La soluzione di questa equazione è facile da ottenere
analiticamente per speciali forme di 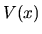 , come ad
esempio nel caso dell'oscillatore armonico; ma in generale
ottenere una soluzione analitica potrebbe risultare assai
laborioso, o impossibile. Ad esempio,
, come ad
esempio nel caso dell'oscillatore armonico; ma in generale
ottenere una soluzione analitica potrebbe risultare assai
laborioso, o impossibile. Ad esempio, 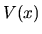 stesso
potrebbe non essere dato in forma analitica, ma solo in
forma di una tabella numerica.
stesso
potrebbe non essere dato in forma analitica, ma solo in
forma di una tabella numerica.
Ma, soprattutto, una volta che siamo in grado di sviluppare
un metodo numerico, potremo estenderlo senza troppa
difficoltà a casi più complessi e
di interesse pratico molto maggiore, come ad esempio un
sistema di molti punti materiali interagenti in tre dimensioni
attraverso interazioni di coppia, o interazioni più complicate.
Subsections




Next: L'algoritmo di Størmer-Verlet
Up: Una applicazione classica
Previous: Una applicazione classica
Contents
furio
2002-02-24
![]() in una dimensione,
soggetto ad un potenziale
in una dimensione,
soggetto ad un potenziale ![]() .
.
![]() )
date la posizione e la velocità iniziali, è la seconda
legge di Newton
)
date la posizione e la velocità iniziali, è la seconda
legge di Newton