STATISTICAL METHODS
The clustering patterns generated by the observed galaxy
distribution have been analyzed in the literature with various statistical
methods. The traditional approach has been the estimate of the two-point
correlation function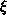 
(r),
which measures the probability in excess of random of finding a galaxy
at distance r from a given one. A more complete clustering description
is obtained by measuring the correlation functions of higher order. Other
statistical indicators have been considered , such as percolation, minimal
spanning tree, topological invariants, multifractal spectrum and Minkowski
functionals. These methods were introduced in order to quantify the
large-scale structure clustering and to check the consistency of theoretical
predictions with clustering data.
In this area I have worked on different subjects:
-
For galaxy clusters the Abell-ACO catalog
was used to measure the amplitude of the 3-point correlation function [1],
the large-scale dipole moment [2], and the topological properties of the
cluster distribution [7].
-
Large-scale cosmological N-body
simulations were used to measure the 3 and 4-point correlation functions
in several theoretical models [3,14].
-
A large number of simulated cluster
catalogs, with low-order statistical properties similar to the Abell-ACO
catalog, was generated for statistical purposes. These catalogs were used
to measure the statistical occurrence of contaminations in the 2-point
cluster correlation function [4], the statistical properties of the large-scale
structure traced by the real cluster distribution [6], the galaxy cluster
power spectrum [9] as well as the cluster distribution function [13].
-
Multifractal analysis has been applied
to the distribution generated from numerical cosmological simulations[5,8,10],
or from cluster data[11].
-
In another paper [14] the point pattern distribution
generated by galaxy catalogs has been studied using the J(r) function,
related to the nearest neighbor search and the void probability function.
The results show that the J statistics can be used to construct
(or reject) models of cosmic structure formation.
-
A new method for analyzing the morphological features of point
patterns is presented in [15]. The method is taken from the study of molecular
liquids, where it has been introduced for making a statistical description of
anisotropic distributions. The statistical approach is based on the
spherical harmonic expansion of angular
correlations .
Related publications:
-
[1] Jing, Y.P., Valdarnini, R., 1991, A determination of the 3-point
spatial correlation function for clusters of galaxies , AA ,250,
1.
-
[2] Plionis, M., Valdarnini, R., 1991, Evidence for Large-Scale Structure
on Scales 300 h-1 Mpc, MNRAS, 249, 46.
-
[3] Valdarnini, R., Borgani ,S. ,1991, Statistical properties of cosmological
N-body simulations , MNRAS, 251, 575.
-
[4] Jing, Y.P., Plionis, M., Valdarnini, R., 1992, Clustering of galaxy
clusters. I. Is the spatial cluster-cluster correlation function enhanced
significantly by contaminations ?, ApJ, 389, 499.
-
[5] Valdarnini, R., Borgani ,S. , Provenzale, A.,1992, Multifractal
properties of cosmological N-body simulations, ApJ, 394, 422.
Plionis, M., Valdarnini, R., Jing, Y.P., 1992, Clustering of galaxy
clusters. II. Rare events in the cluster distribution, ApJ, 398,
12.
-
[6] Plionis, M., Valdarnini, R., Coles, P., 1992, Topology in
two dimension. II. The Abell and the ACO cluster catalogues, MNRAS,
258,
114.
-
[7] Borgani ,S. , Plionis, M., Valdarnini, R., 1993, Multifractal analysis
of cluster distribution in two-dimensions, ApJ, 404, 21.
-
[8] Jing, Y.P., Valdarnini, R., 1993, The Power spectra of IRAS galaxies
and of Abell clusters, ApJ, 406, 6.
-
[9] Borgani, S., Murante, G., Provenzale, A. ,Valdarnini, R.,
1993,
Multifractal analysis of the galaxy distribution : Reliability
from finite data sets, PRE , 47, 3879.
-
[10] Borgani, S., Martinez, V.J., Perez, M.A. & Valdarnini , R. ,1994,
Is there any scaling in the cluster distribution ?, ApJ, 435, 37.
-
[11] Menci, N. & Valdarnini , R. ,1994, Merging rates inside large
scale structures, ApJ., 436, 559.
-
[12] Plionis, M. & Valdarnini , R. ,1995, The 1-Point cluster distribution
function and its moments, MNRAS, 272, 869.
-
[13] Jing, Y.P., B\"orner, G. & Valdarnini, R., 1995, Three-point
correlation function of galaxy clusters in cosmological models: a strong
dependence on triangle shapes, MNRAS, 277, 630.
-
[14] Kerscher, M., Pons-Borderia , M.J., Schmalzing, J., Trasarti-Battistoni,
R., Buchert, T., Martinez, V.J., Valdarnini, R., 1999, A global descriptor
of spatial pattern interaction in the galaxy distribution, ApJ, 513,
543
-
[15] Valdarnini, R., 2001, Detection of non-random patterns in cosmological
gravitational clustering , AA, 366, 376