LIMBO:
Cortical
Attractors
Modular models. The aim is to understand how the organization of memory representations is determined by the underlying plasticity and network connectivity. Early work had considered the simplest modular network model of semantic memory, rejecting it because of inadequate storage capacity [1,2]. A more sophisticated version incorporates the key ingredients, sparsity in module activation and correlations between activation and connectivity, that allow to relieve the capacity limitations [6].
Metric content. To further probe representational structures
and as
an off-shot of information analyses, the metric and ultrametric
structure of discrete perceptual and memory sets has been quantified
with novel
measures, first applied to responses of face cells in the primate
temporal
cortex [3] and of spatial view cells of hippocampal
and parahippocampal
cortices [5]. In an effort to reach towards studies of human performance, we have
shown how to extract such measures
from a
neuropsychological test administered to patients with different types
of memory
disorders [4, 18,19]; while we are studying the effect of the underlying
connectivity
structures on the neuronal and behavioural
response
measures using the above formal network models.
Feedforward self-organization. Analytical techniques
and
simulations have also been applied to formal but realistic models of
self-organizing
competitive networks, aiming at a quantitative understanding of the
functional
properties of this simple type of neuronal organization [7]. The
effects of
learning of the spike count distribution of single cells to large sets
of
stimuli have been predicted using one such model [8].
What and where: lamination. Within the general research goal of attempting to understand the main
evolutionary traits [9] leading from the reptilian to the mammalian
cerebral
cortex, a crucial question has been what drove the emergence of a
laminated neocortex.
Consider the conflict between relaying positional and identity
information by a
model cortical patch [10]. Positional ("where?") information is the
one expressed by the location of activated neurons on the 2D cortical
sheet;
identity ("what?") information is expressed instead in the detailed
activation pattern, at a fixed focus on the sheet. Simulating a
simplified
model patch, including three layers with initially uniform properties,
it was
found that the differentiation of a granular layer with distinct
connectivity
and firing properties leads to a small but reliable quantitative
advantage in
relaying an optimal mixture of both kinds of information. Further, a
differentiation between supra- and infragranular
layers is
shown to optimally match their extrinsic connectivity, thus accounting
for
another advantage which isocortical
lamination may
have brought to mammals [11,12].
If you would like to run the simulations yourself, please ask for the code. Having evolved
lamination in
their topographic sensory cortical systems, mammals went about
multiplying
cortical areas within each system; a model of the advantages this
brought to
the analysis of complex stimuli has been studied using face processing
as an
example [13].
What and where: capacity and stability. A
novel analytical
approach has been
recently developed (YR) to study attractor-mediated retrieval of memory
patterns localized on a cortical patch. Such activity states are still
distributed non-uniformly over many units, but the denser short-range
connectivity allows, beyond a critical line, for the activity to be
concentrated on a restricted patch rather than spread out across the
entire
network [14]. It has been shown analytically and with computer
simulations that
the storage capacity for such localized retrieval states is only
slightly
reduced with respect to that for non-localized retrieval, with the
number of
states still proportional to the number of independently modifiable
synapses
per pyramidal cell [15]. While analytical neural network studies of
attractor
dynamics provide crucial quantitative insight into its power and
limitations,
simulations allow approaching closer to real cortical networks.
Simulations of
Integrate & Fire units in a model network similar to the one
considered
above with non-dynamical units led to divergent results [16],
stimulating an
analysis of the effects of saturation (YR, AA). Moreover, localized
attractor states are found to be unstable to positional drift, and
their theoretical continuity is broken by spatial collapse anto a few
randomly distributed favoured positions - unless a stabilizing signal
is provided, e.g. acting on local neuronal gain [20].
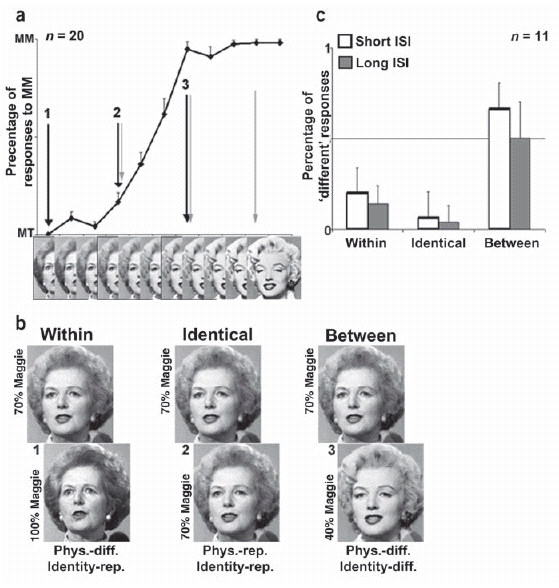
Ambiguity and attractors. Visual processing of facial expressions offers a suitable physiological
model
with which to test predictions arising from mathematical models, also because of the
evidence of parallel processing along a distinct sub-cortical pathway.
This was
the aim of a
Human
Frontier Science Programme collaboration with the labs of Ray
Dolan at UCL and of Bharathi Jagadeesh
at U Washington in
References:
- D O'Kane
& AT, Network 3:379-384
(1992)
- D O'Kane
& AT, Journal of Physics A
25:5055-5069 (1992)
- AT, Biosystems
40:189-196 (1997)
- Papik, C Piccini, F Borgo & AT, Soc Neurosci abs 23:734.2
(1997)
- AT, P Georges-Francois, SP, RG Robertson & ET Rolls, in
Neural Circuits and Networks, NATO ASI series (Springer) Vol F 167: 239-247 (1998)
- CFM & AT, Biosystems
48: 47-55 (1998)
- CFM, SP, GS, ET
& AT, Soc
Neurosci abs 23:197.1 (1997)
- GS & AT, Neural Comp 12:1773-1787
(2000)
- YR & AT, BBS commentary to Principles
of Brain Evolution, by GF Striedter, BBS 29: 23 (2006)
- HM & AT, IBRO World Congress Neurosci abs V:123 (1999)
- AT, Soc Neurosci
abstract 26:739.2 (2000)
- AT, J Comput
Neurosci 14:271-282 (2003)
- AM & AT, Brain Res Bull 60: 387-393 (2003)
- YR & AT, JSTAT P07010 (2004)
- YR & AT, Phys Rev E 73:061904
(2006)
- AA, E Bienenstock
&
AT, preprint (2004)
- P Rotshtein, RNA Henson, AT, J Driver & RJ Dolan, Nature Neurosci 8:107-113 (2005)
- E Ciaramelli, Papik & AT, J Physiol Paris 100: 142-153 (2006)
- Papik, E Ciaramelli, C Piccini & AT, Eur J Neurosci 26:2702-12 (2007)
- YR & AT, PLoS Comput Biol 4(3): e1000012 (2008)
- NvR, AJ & AT, the Open Behavioral Science Journal, 2:36-52 (2008)
- N Furl, NvR, AT & R Dolan, NeuroImage, 37:300–310 (2007)
- N Furl, NvR, AT, K Friston & R Dolan, PNAS USA, 104:13485-9 (2007)
- AAA, Y Liu, AT & B Jagadeesh, Cerebral Cortex, 18:in press (2008)