LIMBO: Latching and Language

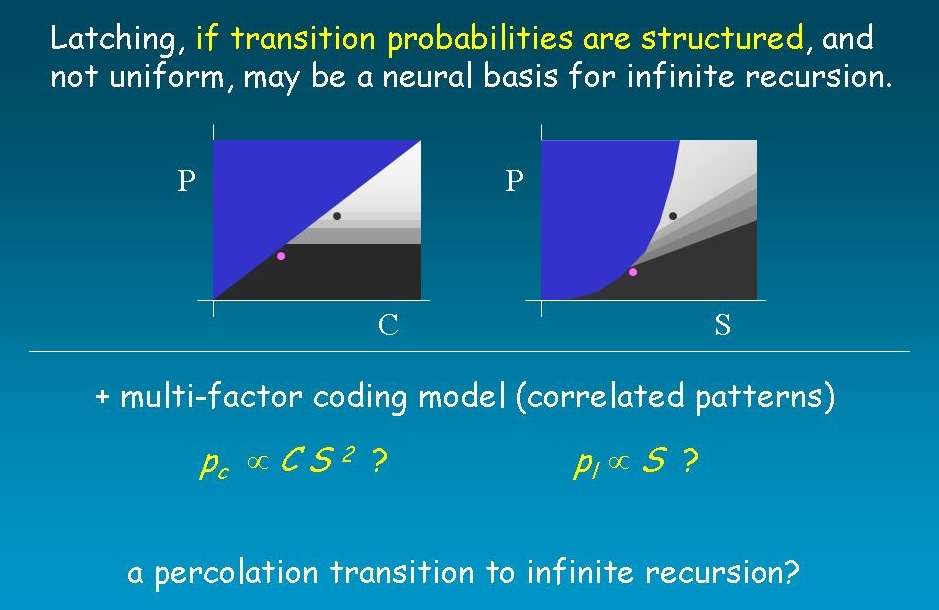
percolation transition in theoryUnderstanding the neural basis of higher cognitive functions, such as those involved in language, in planning, in logics, requires as a very prerequisite a shift from mere localization, which has been popular with imaging research, to an analysis of network operation. A recent proposal (Hauser, Chomsky & Fitch, Science, 2002) points at infinite recursion as the core of several higher functions, and thus challenges cortical network theorists to describe network behavior that could subserve infinite recursion. Considering a class of reduced Potts models (Kanter, PRL, 1988) of large semantic associative networks [1,2], their storage capacity has been studied analytically with statistical physics methods [3,4], and their dynamics simulated, once the units are endowed with a simple model of firing frequency adaptation. Such models naturally display latching dynamics, i.e. they hop from one attractor to the next following a stochastic process based on the correlations among attractors. The proposal is that such latching dynamics may be associated with a network capacity for infinite recursion, in particular because it turns out, from the simulations and from analytical arguments [3], that latching only occurs after a percolation phase transition, once the network connectivity becomes sufficiently extensive to support structured transition probabilities between global network states (work in progress by ER, AT). The crucial development endowing a semantic system with a non-random dynamics would thus be an increase in connectivity, perhaps to be identified with the dramatic increase in spine numbers recently observed in the basal dendrites of pyramidal cells in Old World monkey and particularly in human frontal cortex.

The combinatorial recursion allowed by the latching process is distinct from recursive embedding in syntax, which is a finite form of recursion that might be associated to decaying activity in reverberating assemblies (Pulvermüller, 1999). Following up on previous work with trainable networks [5], we are currently exploring distributed mechanisms of recursion in embeddings, and their interaction with latching combinatorics [6,7]. We have found that already in the simple Potts model latching transitions fall into distinct classes [8], which may provide the basis for rich attractor dynamics in more structured models. 

In a collaboration with Susan Rothstein at Bar Ilan University in Tel Aviv – Ramat Gan, in a violation of the boycott declared by some British teachers, we are analyzing how to reduce language processing to general mechanisms of cortical computation in specific areas, such as the mass/count noun distinction and the syntax of causative constructs.

In parallel, we are conducting psychophysical experiments that closely model those by Onnis et al (2003), on the influence of variability in the statistical learning of correlations (NvR & AG).

References:

  1. D O'Kane & AT, Network 3:379-384 (1992)
  2. CFM & AT, Biosystems 48: 47-55 (1998)
  3. AT, Cognitive Neuropsychology 21:276-291 (2005)  You may also ask for a reprint
  4. EK & AT, JSTAT  2:P08010  (2005)
  5. AG, Stack- and queue-like dynamics in recurrent neural networks, Connection Science 18:in press (2006)
  6. AG & AT, BBS commentary to the target article by van der Velde & de Kamps (2006)
  7. EK & AT, Natural Computing 10.1007/s11047-006-9019-3 (2007)
  8. ER, VN, AT & EK, New Journal of Physics 10: 015008 (2008)
  9. Eleonora
  10. Sahar
  11. Ritwik... see News and Events till I manage to update these pages, thanks
Last updated 06/07/08. Back to LIMBO, CNS, SISSA.