| (2.3) |
Prima di procedere, ricordiamo il legame fra l'equazione di
Schrödinger indipendente dal tempo (2.1), e quella
più generale dipendente dal tempo
Nel caso in cui il potenziale ![]() non dipenda dal tempo, si
può provare a esprimere la soluzione come un prodotto di
una funzione di solo
non dipenda dal tempo, si
può provare a esprimere la soluzione come un prodotto di
una funzione di solo ![]() e una di solo
e una di solo ![]() :
:
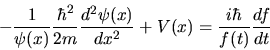 |
(2.5) |
| (2.6) |
| (2.7) |
Abbiamo quindi trovato che ad ogni soluzione ![]() della
(2.1), corrispondente a un certo valore di
della
(2.1), corrispondente a un certo valore di ![]() ,
corrisponde anche una soluzione della (2.3)
,
corrisponde anche una soluzione della (2.3)
Inoltre, ricordando che uno dei postulati della meccanica
quantistica è che la quantità di moto lungo la
direzione ![]() sia rappresentata dall'operatore
sia rappresentata dall'operatore
![]() , la (2.1) può anche essere scritta
, la (2.1) può anche essere scritta
![\begin{displaymath}
\left[ \frac{p^2}{2m} + V(x) \right] \psi(x) = E\psi(x)
\end{displaymath}](img62.gif) |
(2.9) |
![]() data dalla (2.8) non è una
soluzione generale dell'equazione di Schrödinger dipendente dal
tempo (2.3). Tuttavia, si può dimostrare che
l'insieme di tutte le soluzioni possibili è costituito
dalle combinazioni lineari delle autofunzioni dell'energia, ossia
qualsiasi soluzione
data dalla (2.8) non è una
soluzione generale dell'equazione di Schrödinger dipendente dal
tempo (2.3). Tuttavia, si può dimostrare che
l'insieme di tutte le soluzioni possibili è costituito
dalle combinazioni lineari delle autofunzioni dell'energia, ossia
qualsiasi soluzione ![]() è
sempre esprimibile come una sovrapposizione di stati stazionari:
è
sempre esprimibile come una sovrapposizione di stati stazionari:
Questo è un risultato importante: data una funzione d'onda
![]() che si sa essere una soluzione valida ad un certo istante
che si sa essere una soluzione valida ad un certo istante
![]() , la sua evoluzione temporale può essere ottenuta
facilmente se si riesce a espanderla in stati stazionari
al tempo
, la sua evoluzione temporale può essere ottenuta
facilmente se si riesce a espanderla in stati stazionari
al tempo ![]() secondo la (2.10).
secondo la (2.10).
La soluzione numerica diretta [ossia operando nello
spazio ![]() ] dell'equazione (2.3) è in
generale un problema difficile, che porta spesso a
instabilità numeriche.
Quasi sempre l'evoluzione temporale di una funzione d'onda
non corrispondente ad uno stato stazionario viene perciò studiata
decomponendola in autofunzioni dell'energia--la cui evoluzione
temporale è data dalla (2.8)--secondo la
(2.10).
] dell'equazione (2.3) è in
generale un problema difficile, che porta spesso a
instabilità numeriche.
Quasi sempre l'evoluzione temporale di una funzione d'onda
non corrispondente ad uno stato stazionario viene perciò studiata
decomponendola in autofunzioni dell'energia--la cui evoluzione
temporale è data dalla (2.8)--secondo la
(2.10).
Tuttavia, nel caso generale in cui il potenziale dipende dal tempo la separazione delle variabili non è possibile, e il problema va quindi affrontato risolvendo direttamente la (2.3).