



Next: Atomi con un elettrone
Up: Composizione di momenti angolari:
Previous: Esempio: singoletti e tripletti
Contents
Perchè abbiamo introdotto questa rappresentazione, apparentemente
equivalente a quella che considera i due momenti angolari separatamente?
Il motivo è che in molti casi sono presenti termini
nell'hamiltoniana che accoppiano i momenti angolari tra loro.
Comune è ad esempio il caso di una ``coppia'' che tende ad
allineare i due vettori:
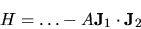 |
(3.120) |
In presenza di tale termine, 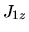 e
e 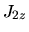 non sono più
conservati, ossia non sono più buoni numeri quantici. Infatti
non sono più
conservati, ossia non sono più buoni numeri quantici. Infatti
e questo operatore in generale non è nullo.
Viceversa, è immediato vedere che
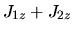 è
conservato, in quanto
è
conservato, in quanto
![$[J_{2z}, - A {\bf J}_1 \cdot {\bf J}_2]$](img512.gif) risulta essere uguale al termine calcolato qua sopra con
segno opposto.
risulta essere uguale al termine calcolato qua sopra con
segno opposto.




Next: Atomi con un elettrone
Up: Composizione di momenti angolari:
Previous: Esempio: singoletti e tripletti
Contents
furio
2002-02-24
![]() è
conservato, in quanto
è
conservato, in quanto
![]() risulta essere uguale al termine calcolato qua sopra con
segno opposto.
risulta essere uguale al termine calcolato qua sopra con
segno opposto.