Consideriamo un sistema in cui ![]() e
e ![]() sono
due operatori momento angolare che commutano tra loro.
Ciò accade quando si riferiscono a sistemi fisici indipendenti;
ad esempio i momenti angolari di due particelle diverse, oppure
il momento angolare orbitale e quello di spin di una stessa
particella nell'assunzione che non vi siano interazioni che li
accoppiano.
Avremo quindi quattro osservabili commutanti per descrivere
il sistema:
sono
due operatori momento angolare che commutano tra loro.
Ciò accade quando si riferiscono a sistemi fisici indipendenti;
ad esempio i momenti angolari di due particelle diverse, oppure
il momento angolare orbitale e quello di spin di una stessa
particella nell'assunzione che non vi siano interazioni che li
accoppiano.
Avremo quindi quattro osservabili commutanti per descrivere
il sistema: ![]() ,
, ![]() ,
, ![]() e
e ![]() , e
gli autostati comuni saranno caratterizzati dall'insieme di
numeri quantici
, e
gli autostati comuni saranno caratterizzati dall'insieme di
numeri quantici ![]() ,
, ![]() ,
, ![]() e
e ![]() .
Dati
.
Dati ![]() e
e ![]() , avremno quindi
, avremno quindi
![]() stati
distinti.
stati
distinti.
Esiste anche un'altro utile insieme di osservabili per
descrivere lo stesso sistema. Definiamo l'operatore
momento angolare totale
| (3.115) |
![\begin{displaymath}
\begin{array}{rcl}
[J_x,J_y] & = & [J_{1x} + J_{2x}, J_{1y} ...
... i\hbar J_{1z} + i\hbar J_{2z} \\
& = & i\hbar J_z
\end{array}\end{displaymath}](img482.gif) |
(3.116) |
Possiamo descrivere allora il sistema anche usando i
quattro operatori ![]() ,
, ![]() ,
, ![]() e
e ![]() .
Si tratta della cosiddetta rappresentazione accoppiata
(il motivo di questo nome sarà chiaro tra breve).
Per dimostrare che commutano tutti fra loro ci resta da
vedere che
.
Si tratta della cosiddetta rappresentazione accoppiata
(il motivo di questo nome sarà chiaro tra breve).
Per dimostrare che commutano tutti fra loro ci resta da
vedere che
![]() , e che
, e che
![]() .
.
![\begin{displaymath}
\begin{array}{rcl}
[J_1^2,J^2] & = & [J_1^2,J_x J_x + J_y J_...
...J_{1x}] + [J_1^2,J_{1x}] J_x + (\ldots) \\
& = & 0
\end{array}\end{displaymath}](img486.gif) |
(3.117) |
![\begin{displaymath}
\begin{array}{rcl}
[J_1^2,J_z] & = & [J_1^2, J_{1z} + J_{2z}] \\
& = & [J_1^2, J_{1z}] \\
& = & 0
\end{array}\end{displaymath}](img487.gif) |
(3.118) |
![]() è la proiezione di
è la proiezione di
![]() , e quindi per
definizione dovrà essere
, e quindi per
definizione dovrà essere ![]() . Da questo si desume
che il massimo valore possibile per
. Da questo si desume
che il massimo valore possibile per ![]() è
è ![]() , ma
il massimo valore possibile per
, ma
il massimo valore possibile per ![]() è anche pari a
è anche pari a ![]() .
Dunque
.
Dunque
![]() .
.
![]() si ottiene imponendo che il numero totale di stati sia lo
stesso ottenuto nella prima rappresentazione:
si ottiene imponendo che il numero totale di stati sia lo
stesso ottenuto nella prima rappresentazione:
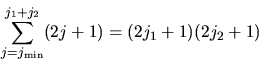 |
(3.119) |
Dunque
![]() . Si può pensare che
nel caso
. Si può pensare che
nel caso ![]() i due vettori abbiano la stessa direzione
ma verso opposto, e nel caso
i due vettori abbiano la stessa direzione
ma verso opposto, e nel caso ![]() la stessa direzione
e verso; i casi intermedi corrispondono a momenti angolari
che puntano in direzioni diverse.
la stessa direzione
e verso; i casi intermedi corrispondono a momenti angolari
che puntano in direzioni diverse.