Densità radiale

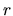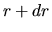La probabilità di trovare la particella a una distanza compresa tra $r$ e $r+dr$ dal centro è ottenuta integrando sulle variabili angolari:

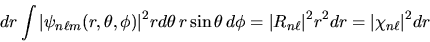$$dr \int \vert\psi_{n\ell m}(r,\theta,\phi)\vert^2 r d\theta\... ... = \vert R_{n\ell}\vert^2 r^2 dr = \vert\chi_{n\ell}\vert^2 dr$$ (4.40)

avendo sfruttato la proprietà di normalizzazione delle armoniche sferiche

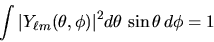$$\int \vert Y_{\ell m} (\theta,\phi)\vert^2 d\theta \sin\theta d\phi = 1$$ (4.41)

(dove l'integrazione è estesa a tutti i possibili angoli). Ne segue anche che la condizione di normalizzazione in termini di 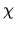$\chi$ è

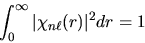$$\int_0^\infty \vert\chi_{n\ell}(r)\vert^2 dr = 1$$ (4.42)

La funzione 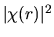$\vert\chi(r)\vert^2$ può essere dunque direttamente interpretata come una densità radiale.