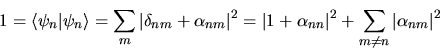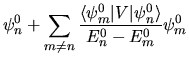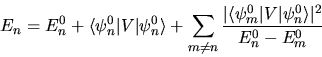Next: Esempio: trattamento perturbativo dell'atomo
Up: Metodi approssimati
Previous: Metodi approssimati
Contents
Metodo perturbativo
Supponiamo che l'hamiltoniano possa essere scritto in forma
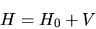 |
(5.1) |
dove 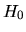 è un ``hamiltoniano di riferimento'' i cui autostati
si suppone noti:
è un ``hamiltoniano di riferimento'' i cui autostati
si suppone noti:
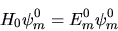 |
(5.2) |
e 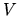 una ``perturbazione'' che supporremo piccola, e indipendente
dal tempo. Supporremo inoltre che non vi sia degenerazione,
ossia che gli
una ``perturbazione'' che supporremo piccola, e indipendente
dal tempo. Supporremo inoltre che non vi sia degenerazione,
ossia che gli 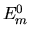 siano tutti diversi (il caso in cui vi
è degenerazione si può pure trattare senza troppa difficoltà).
siano tutti diversi (il caso in cui vi
è degenerazione si può pure trattare senza troppa difficoltà).
Consideriamo le soluzioni del problema completo:
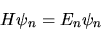 |
(5.3) |
Poichè le 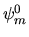 costituiscono un insieme completo, è di
certo possibile espandere le
costituiscono un insieme completo, è di
certo possibile espandere le 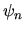 secondo
secondo
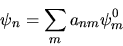 |
(5.4) |
Con questa posizione la (5.3) diventa
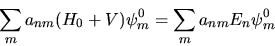 |
(5.5) |
da cui
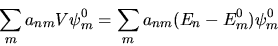 |
(5.6) |
Moltiplichiamo a sinistra per 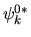 e integriamo.
Utilizziamo per brevità la notazione di Dirac
e integriamo.
Utilizziamo per brevità la notazione di Dirac
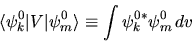 |
(5.7) |
(integrato su tutte le coordinate).
Si ottiene, sfruttando l'ortonormalità delle 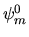 ,
,
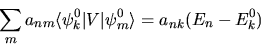 |
(5.8) |
Fino a questo momento non è stata effettuata alcuna approssimazione.
Poniamo ora
ottenendo
e supponiamo che 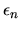 e
e 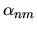 , assieme
agli integrali (5.7), siano delle quantità
piccole. Approssimiamo al primo ordine (eliminando cioè
tutti i termini di ordine successivo al primo):
, assieme
agli integrali (5.7), siano delle quantità
piccole. Approssimiamo al primo ordine (eliminando cioè
tutti i termini di ordine successivo al primo):
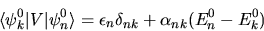 |
(5.13) |
Nel caso 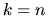 abbiamo
abbiamo
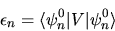 |
(5.14) |
Questo è un risultato molto importante, che ci permette di
ottenere rapidamente una stima del cambiamento di autovalore
conseguente a una perturbazione mediante integrali sugli
stati imperturbati.
Il caso 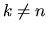 ci dà
ci dà
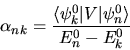 |
(5.15) |
che pure ha una interpretazione fisica: uno stato 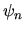 è ottenuto come ``miscela'' degli stati imperturbati,
di cui
è ottenuto come ``miscela'' degli stati imperturbati,
di cui 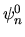 costituisce l'ingrediente
fondamentale, e in cui gli altri
costituisce l'ingrediente
fondamentale, e in cui gli altri 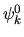 appaiono
con coefficienti proporzionali all'"accoppiamento"
tra
appaiono
con coefficienti proporzionali all'"accoppiamento"
tra 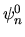 e
e 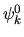 attraverso la perturbazione,
e inversamente proporzionali alla differenza di energia.
attraverso la perturbazione,
e inversamente proporzionali alla differenza di energia.
Notiamo che al primo ordine deve essere
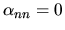 .
Infatti
.
Infatti
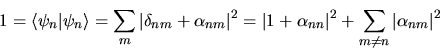 |
(5.16) |
Al primo ordine il membro a destra è
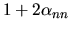 , da cui l'asserto.
, da cui l'asserto.
Riassumendo, i risultati della teoria delle perturbazioni non
dipendenti dal tempo al primo ordine sono
È naturalmente possibile sviluppare la teoria delle
perturbazioni ad ordini più elevati. Ad esempio al
secondo ordine si trova
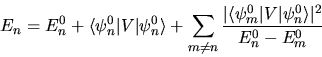 |
(5.19) |
Subsections




Next: Esempio: trattamento perturbativo dell'atomo
Up: Metodi approssimati
Previous: Metodi approssimati
Contents
furio
2002-02-24
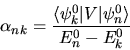
![]() .
Infatti
.
Infatti