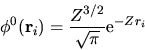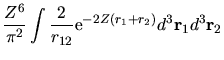Next: Metodo variazionale
Up: Metodo perturbativo
Previous: Metodo perturbativo
Contents
Esempio: trattamento perturbativo dell'atomo di elio
L'atomo di elio è caratterizzato da un hamiltoniano
(in unità atomiche basate sul Rydberg)
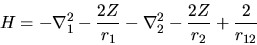 |
(5.20) |
dove
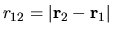 è la
distanza tra i due elettroni.
L'ultimo termine, corrispondente alla repulsione coulombiana tra
i due elettroni, li accoppia tra loro e rende il
problema non separabile.
è la
distanza tra i due elettroni.
L'ultimo termine, corrispondente alla repulsione coulombiana tra
i due elettroni, li accoppia tra loro e rende il
problema non separabile.
In prima approssimazione è possibile però considerare
l'interazione tra elettroni
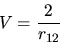 |
(5.21) |
come una perturbazione al problema descritto da
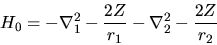 |
(5.22) |
che è facile da risolvere in quanto si separa in due problemi
di un singolo elettrone in un campo di forze centrale
coulombiano, ossia il problema di un atomo idrogenoide con
nucleo di carica 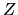 .
Lo stato fondamentale di un singolo elettrone è dato da una
funzione del tipo (4.43):
.
Lo stato fondamentale di un singolo elettrone è dato da una
funzione del tipo (4.43):
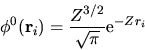 |
(5.23) |
("orbitale 1s"). Notiamo che possiamo assegnare ad entrambi
gli elettroni la stessa funzione d'onda, purchè il loro
spin sia opposto (se il loro spin fosse uguale, uno dei due
dovrebbe essere portato in uno stato eccitato altrimenti il
principio di esclusione verrebbe violato).
La funzione d'onda totale imperturbata è allora semplicemente
il prodotto
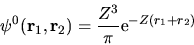 |
(5.24) |
che è già una funzione simmetrica.
L'energia del corrispondente stato fondamentale sarà la somma
delle energie dei due atomi idrogenoidi:
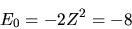 |
(5.25) |
essendo 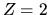 .
La repulsione tra elettroni dovrà alzare l'energia, rendendola
cioè meno negativa. Nella teoria delle perturbazioni al primo
ordine,
.
La repulsione tra elettroni dovrà alzare l'energia, rendendola
cioè meno negativa. Nella teoria delle perturbazioni al primo
ordine,
come si ottiene calcolando l'integrale.
Per 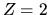 la correzione è pari a 2.5 Ry, e fornisce un'energia
la correzione è pari a 2.5 Ry, e fornisce un'energia
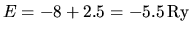 . Il valore sperimentale è pari a
. Il valore sperimentale è pari a
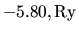 . L'approssimazione perturbativa non è
precisa, ma fornisce una stima ragionevole della correzione
pur essendo la ``perturbazione'' in questo caso di notevole entità.
. L'approssimazione perturbativa non è
precisa, ma fornisce una stima ragionevole della correzione
pur essendo la ``perturbazione'' in questo caso di notevole entità.




Next: Metodo variazionale
Up: Metodo perturbativo
Previous: Metodo perturbativo
Contents
furio
2002-02-24