



Next: Dimostrazione del principio variazionale
Up: Metodo variazionale
Previous: Metodo variazionale
Contents
Dimostrazione del principio variazionale (I)
Poichè una variazione arbitraria 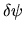 di una
funzione d'onda in generale ne distrugge la normalizzazione,
è conveniente utilizzare la definizione più generale
di valor medio
di una
funzione d'onda in generale ne distrugge la normalizzazione,
è conveniente utilizzare la definizione più generale
di valor medio
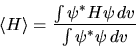 |
(5.30) |
Modificando la 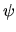 in
in
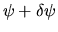 , il valor medio diventa
, il valor medio diventa
dove si sono omessi i termini del secondo ordine in 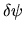 ,
e si è usata l'approssimazione
,
e si è usata l'approssimazione
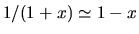 valida per piccoli
valida per piccoli 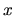 .
Pertanto
.
Pertanto
![\begin{displaymath}
\delta \langle H\rangle =
\int \delta\psi^* H \psi dv + \...
...\delta\psi^* \psi dv + \int \psi^* \delta\psi dv
\right]
\end{displaymath}](img719.gif) |
(5.32) |
I due termini nella parentesi quadra sono l'uno il complesso
coniugato dell'altro, e lo stesso vale anche per i primi due
poichè 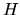 è un operatore hermitiano, e soddisfa quindi a
è un operatore hermitiano, e soddisfa quindi a
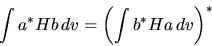 |
(5.33) |
per qualsiasi coppia di funzioni 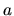 e
e 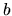 . Pertanto
. Pertanto
![\begin{displaymath}
\delta \langle H\rangle =
\left[ \int \delta\psi^* H \psi ...
...angle \left[
\int \delta\psi^* \psi dv + {\rm c.c.} \right]
\end{displaymath}](img721.gif) |
(5.34) |
Supponiamo ora che 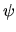 sia tale che
sia tale che
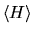 sia stazionario rispetto a qualsiasi sua variazione.
Sarà allora
sia stazionario rispetto a qualsiasi sua variazione.
Sarà allora
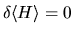 , ossia
, ossia
![\begin{displaymath}
\int \delta\psi^* \left[
H - \langle H\rangle \right] \psi dv + {\rm c.c.} = 0
\end{displaymath}](img723.gif) |
(5.35) |
per una variazione 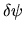 arbitraria, e questo
implica che deve essere
arbitraria, e questo
implica che deve essere
![\begin{displaymath}
\left[ H - \langle H\rangle \right] \psi = 0
\end{displaymath}](img724.gif) |
(5.36) |
ovvero 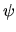 è una soluzione dell'equazione di Schrödinger:
è una soluzione dell'equazione di Schrödinger:
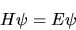 |
(5.37) |




Next: Dimostrazione del principio variazionale
Up: Metodo variazionale
Previous: Metodo variazionale
Contents
furio
2002-02-24
![]() di una
funzione d'onda in generale ne distrugge la normalizzazione,
è conveniente utilizzare la definizione più generale
di valor medio
di una
funzione d'onda in generale ne distrugge la normalizzazione,
è conveniente utilizzare la definizione più generale
di valor medio
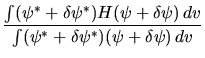
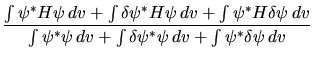
![$\displaystyle \left[ \langle H\rangle +
\int \delta\psi^* H \psi dv +
\int \psi^* H \delta\psi dv \right] \times$](img716.gif)
![$\displaystyle \left[ 1 -
\int \delta\psi^* \psi dv -
\int \psi^* \delta\psi dv \right]$](img717.gif)
![]() sia tale che
sia tale che
![]() sia stazionario rispetto a qualsiasi sua variazione.
Sarà allora
sia stazionario rispetto a qualsiasi sua variazione.
Sarà allora
![]() , ossia
, ossia