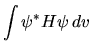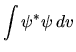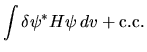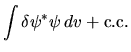Next: Energia dello stato fondamentale
Up: Metodo variazionale
Previous: Dimostrazione del principio variazionale
Contents
Dimostrazione del principio variazionale (II)
Un altro modo di dimostrare lo stesso principio, utile in
seguito, è basato sul metodo dei moltiplicatori di Lagrange.
Il metodo afferma che se si vuole rendere stazionario un
integrale 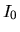 mantenendo allo stesso tempo costanti
altri integrali
mantenendo allo stesso tempo costanti
altri integrali
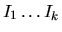 , si può porre
, si può porre
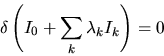 |
(5.38) |
dove 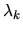 sono costanti da determinare.
Nel nostro caso avremo
sono costanti da determinare.
Nel nostro caso avremo
e quindi porremo
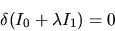 |
(5.41) |
con 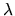 da determinare.
Procedendo come nella sezione precedente si ha
da determinare.
Procedendo come nella sezione precedente si ha
e quindi la condizione da soddisfare è
![\begin{displaymath}
\delta(I_0 + \lambda I_1) =
\int \delta\psi^* [ H + \lambda ] \psi dv + {\rm c.c.} = 0
\end{displaymath}](img740.gif) |
(5.44) |
da cui
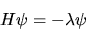 |
(5.45) |
ossia il moltiplicatore di Lagrange è uguale, a meno del
segno, a un autovalore dell'energia.
Nuovamente vediamo che gli stati la cui energia media è
stazionaria rispetto a qualsiasi variazione della funzione
d'onda sono le soluzioni dell'equazione di Schrödinger.




Next: Energia dello stato fondamentale
Up: Metodo variazionale
Previous: Dimostrazione del principio variazionale
Contents
furio
2002-02-24
![]() mantenendo allo stesso tempo costanti
altri integrali
mantenendo allo stesso tempo costanti
altri integrali
![]() , si può porre
, si può porre