



Next: Caso di più particelle
Up: Atomi a più elettroni
Previous: Particelle identiche: principio di
Contents
Consideriamo un sistema a due particelle e chiamiamo 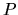 l'operatore che le scambia. Ossia:
l'operatore che le scambia. Ossia:
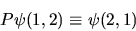 |
(6.5) |
per qualsiasi funzione d'onda.
Ovviamente 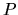 è un "operatore idempotente", ossia
soddisfa a
è un "operatore idempotente", ossia
soddisfa a 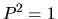 , e anche
, e anche
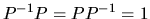 .
.
Il principio di indistinguibilità ci dice che qualsiasi
misura deve dare lo stesso risultato se effettuata sullo
stato 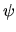 o sullo stato
o sullo stato 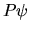 . Se l'operatore
. Se l'operatore 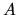 corrisponde ad una generica osservabile e il sistema è in
un autostato di
corrisponde ad una generica osservabile e il sistema è in
un autostato di 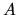 :
:
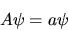 |
(6.6) |
(ossia, una misura di 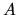 dà come risultato un numero
dà come risultato un numero
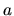 ben definito), allora deve anche essere vero che
ben definito), allora deve anche essere vero che
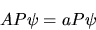 |
(6.7) |
D'altra parte applicando l'operatore P a sinistra e a destra
nella prima equazione si ha anche
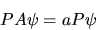 |
(6.8) |
Sottraendo tra loro le ultime due equazioni e notando che
questo deve valere per qualsiasi stato fisico 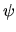 ,
deve allora essere
,
deve allora essere
![\begin{displaymath}[P,A]= 0
\end{displaymath}](img874.gif) |
(6.9) |
ossia l'operatore 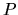 deve commutare con qualsiasi osservabile
fisica, inclusa l'energia:
deve commutare con qualsiasi osservabile
fisica, inclusa l'energia:
![\begin{displaymath}[P,H]= 0
\end{displaymath}](img875.gif) |
(6.10) |
e quindi è una quantità conservata. Da quanto sopra si
inferisce inoltre che i suoi valori possono essere
solamente 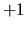 oppure
oppure 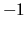 .
.
Risulta che il segno dell'autovalore dell'operatore di
scambio, o parità, è una proprietà intrinseca
del tipo di particella. Le particelle si dividono in
- bosoni:
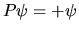
- fermioni:
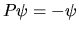
dove 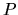 è riferito a una qualsiasi coppia di particelle
di quel tipo. Un insieme di particelle si comporta
dunque sempre in un dato modo, che dipende esclusivamente
dal carattere di bosone o fermione della particella.
è riferito a una qualsiasi coppia di particelle
di quel tipo. Un insieme di particelle si comporta
dunque sempre in un dato modo, che dipende esclusivamente
dal carattere di bosone o fermione della particella.




Next: Caso di più particelle
Up: Atomi a più elettroni
Previous: Particelle identiche: principio di
Contents
furio
2002-02-24
![]() l'operatore che le scambia. Ossia:
l'operatore che le scambia. Ossia:
![]() o sullo stato
o sullo stato ![]() . Se l'operatore
. Se l'operatore ![]() corrisponde ad una generica osservabile e il sistema è in
un autostato di
corrisponde ad una generica osservabile e il sistema è in
un autostato di ![]() :
: