



Next: Programma: helium_hf
Up: Il metodo di Hartree-Fock
Previous: Il metodo di Hartree-Fock
Contents
Esaminiamo il termine di scambio:
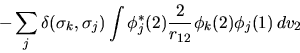 |
(6.46) |
A differenza del termine di Hartree, non ha la forma
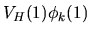 ,
dove
,
dove 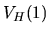 contiene l'integrazione sulla variabile 2.
Ha piuttosto una forma del tipo
contiene l'integrazione sulla variabile 2.
Ha piuttosto una forma del tipo
che caratterizza una interazione non locale.
Per cercare di comprendere questo termine, definiamo la seguente
``densità di scambio'':
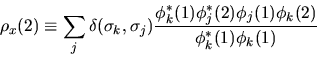 |
(6.47) |
Con questa definizione, il termine di scambio (6.46) si
può riscrivere
![\begin{displaymath}
- \left[ \int \rho_x(2) \frac{2}{r_{12}} \, dv_2 \right] \phi_k(1)
\end{displaymath}](img969.gif) |
(6.48) |
Lo scopo di questa definizione un po' artificiosa è stato
quello di riuscire a scrivere formalmente il termine di
scambio come il prodotto di un ``potenziale efficace'' per 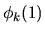 ,
risultante da interazioni elettrostatiche con una
distribuzione spaziale di densità di carica, esattamente
come abbiamo fatto per il termine di Hartree.
,
risultante da interazioni elettrostatiche con una
distribuzione spaziale di densità di carica, esattamente
come abbiamo fatto per il termine di Hartree.
La densità di scambio ha le seguenti proprietà:
- vi contribuiscono solo gli elettroni con lo stesso spin
di quello che stiamo considerando
- rappresenta una quantità di carica totale pari a 1.
Infatti
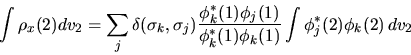 |
(6.49) |
da cui si vede che i termini con 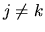 danno contributo nullo,
mentre quello con
danno contributo nullo,
mentre quello con 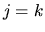 dà un contributo pari a uno.
Questa carica è dunque quella
dell'elettrone che sto considerando, ma distribuita in qualche
modo nello spazio.
Da notare che se considero uno stato
dà un contributo pari a uno.
Questa carica è dunque quella
dell'elettrone che sto considerando, ma distribuita in qualche
modo nello spazio.
Da notare che se considero uno stato 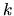 eccitato, ossia non
occupato, allora è sempre
eccitato, ossia non
occupato, allora è sempre 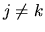 e la carica di scambio è nulla,
come si conviene ad un elettrone ...che non c'è.
e la carica di scambio è nulla,
come si conviene ad un elettrone ...che non c'è.
- esaminiamo cosa succede quando i punti 1 e 2 tendono a coincidere.
In questo limite la carica di scambio tende a
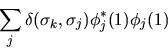 |
(6.50) |
ossia alla densità totale nel punto 1 di tutti gli elettroni
con lo stesso spin dell'elettrone 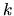 .
.
Vediamo dunque che, nell'equazione di Hartree-Fock per
l'elettrone 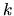 , il primo
termine (quello di Hartree, ma con somma estesa a tutti i
, il primo
termine (quello di Hartree, ma con somma estesa a tutti i 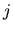 )
include le interazioni efficaci con tutti gli elettroni,
incluso
)
include le interazioni efficaci con tutti gli elettroni,
incluso 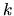 . Il termine di scambio toglie l'interazione
dell'elettrone che stiamo considerando con se stesso.
. Il termine di scambio toglie l'interazione
dell'elettrone che stiamo considerando con se stesso.
Consideriamo ora la densità di carica totale (Hartree+scambio)
con lo stesso spin dell'elettrone 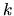 . Questa densità
è nulla nel punto in cui si trova
. Questa densità
è nulla nel punto in cui si trova 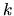 , perchè in quel punto
il termine di scambio compensa esattamente il termine di Hartree
come indicato dall'ultima proprietà sopra.
Quindi è come se il nostro elettrone trascinasse con sè
una buca, detta buca di Fermi, che tiene lontani gli
altri elettroni con lo stesso spin. Si tratta ovviamente
di un effetto dovuto al principio di esclusione.
, perchè in quel punto
il termine di scambio compensa esattamente il termine di Hartree
come indicato dall'ultima proprietà sopra.
Quindi è come se il nostro elettrone trascinasse con sè
una buca, detta buca di Fermi, che tiene lontani gli
altri elettroni con lo stesso spin. Si tratta ovviamente
di un effetto dovuto al principio di esclusione.
Notiamo infine che il metodo di Hartree il termine escluso
dalla somma 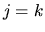 esclude--in modo più rudimentale--l'interazione
dell'elettrone
esclude--in modo più rudimentale--l'interazione
dell'elettrone 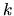 con se stesso: lo stesso effetto rappresentato
dal termine di scambio nelle equazioni di Hartree-Fock.
con se stesso: lo stesso effetto rappresentato
dal termine di scambio nelle equazioni di Hartree-Fock.




Next: Programma: helium_hf
Up: Il metodo di Hartree-Fock
Previous: Il metodo di Hartree-Fock
Contents
furio
2002-02-24
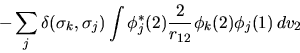
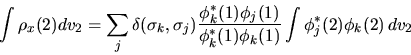
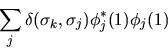
![]() , il primo
termine (quello di Hartree, ma con somma estesa a tutti i
, il primo
termine (quello di Hartree, ma con somma estesa a tutti i ![]() )
include le interazioni efficaci con tutti gli elettroni,
incluso
)
include le interazioni efficaci con tutti gli elettroni,
incluso ![]() . Il termine di scambio toglie l'interazione
dell'elettrone che stiamo considerando con se stesso.
. Il termine di scambio toglie l'interazione
dell'elettrone che stiamo considerando con se stesso.
![]() . Questa densità
è nulla nel punto in cui si trova
. Questa densità
è nulla nel punto in cui si trova ![]() , perchè in quel punto
il termine di scambio compensa esattamente il termine di Hartree
come indicato dall'ultima proprietà sopra.
Quindi è come se il nostro elettrone trascinasse con sè
una buca, detta buca di Fermi, che tiene lontani gli
altri elettroni con lo stesso spin. Si tratta ovviamente
di un effetto dovuto al principio di esclusione.
, perchè in quel punto
il termine di scambio compensa esattamente il termine di Hartree
come indicato dall'ultima proprietà sopra.
Quindi è come se il nostro elettrone trascinasse con sè
una buca, detta buca di Fermi, che tiene lontani gli
altri elettroni con lo stesso spin. Si tratta ovviamente
di un effetto dovuto al principio di esclusione.
![]() esclude--in modo più rudimentale--l'interazione
dell'elettrone
esclude--in modo più rudimentale--l'interazione
dell'elettrone ![]() con se stesso: lo stesso effetto rappresentato
dal termine di scambio nelle equazioni di Hartree-Fock.
con se stesso: lo stesso effetto rappresentato
dal termine di scambio nelle equazioni di Hartree-Fock.