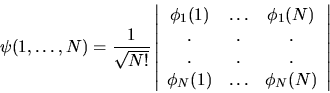 |
(6.37) |
Il metodo di Hartree, che si basa sull'assunzione (6.26),
costruisce una funzione d'onda totale che non ha la proprietà
di essere antisimmetrica per scambio di una coppia.
In base a quanto discusso all'inizio di questo capitolo,
è evidente come sia più desiderabile lavorare con
una forma antisimmetrica, ossia con un determinante di Slater:
Si può ripercorrere per la (6.37) tutto lo
schema seguito per arrivare alle equazioni di Hartree
(6.33). Le complicazioni sono puramente algebriche,
legate alla funzione determinantale.
È di molto aiuto la proprietà, valida per qualsiasi
operatore ![]() e funzioni determinantali
e funzioni determinantali ![]() e
e ![]() :
:
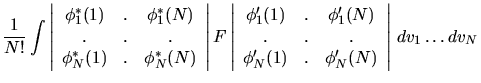 |
|||
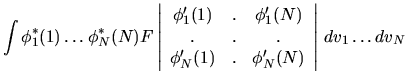 |
(6.38) |
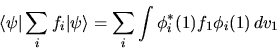 |
(6.39) |
| (6.41) |
Passando ad uno schema in cui invece le variabili di spin non
sono esplicitamente incluse, la (6.40) si può scrivere
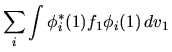 |
(6.43) | ||
![$\displaystyle \sum_{\langle ij\rangle}
\int \phi_i^*(1) \phi_j^*(2) g_{12}
\lef...
...\phi_j(2) -
\delta(\sigma_i, \sigma_j) \phi_j(1) \phi_i(2) \right]
\, dv_1 dv_2$](img956.gif) |
Si procede quindi all'applicazione del principio variazionale,
A rigore è necessario imporre non solo che tutte le
![]() restino normalizzate a 1, ma anche che tutte le
coppie
restino normalizzate a 1, ma anche che tutte le
coppie ![]() ,
, ![]() con lo stesso spin restino fra loro
ortogonali. Quest'ultima condizione non era necessaria per
il metodo di Hartree e per questo motivo non l'abbiamo menzionata
prima. Questo genera una matrice (triangolare) di
moltiplicatori di Lagrange
con lo stesso spin restino fra loro
ortogonali. Quest'ultima condizione non era necessaria per
il metodo di Hartree e per questo motivo non l'abbiamo menzionata
prima. Questo genera una matrice (triangolare) di
moltiplicatori di Lagrange ![]() . Tuttavia, si può
far vedere (i dettagli sono sul libro di Slater [4])
che si può sempre pensare di prendere una soluzione per
cui la matrice degli
. Tuttavia, si può
far vedere (i dettagli sono sul libro di Slater [4])
che si può sempre pensare di prendere una soluzione per
cui la matrice degli ![]() è diagonale mediante una
semplice trasformazione.
è diagonale mediante una
semplice trasformazione.
Omettiamo i dettagli e diamo direttamente le risultanti equazioni di Hartree-Fock, ottenute al solito pensando di
variare una sola funzione ![]() :
:
Osserviamo attentamente le differenze rispetto alle equazioni di Hartree (6.33):
Prima di procedere osserviamo che la (6.45)
avrà normalmente infinite soluzioni, di cui solo le ![]() a energia più bassa verranno occupate da elettroni.
Gli stati che restano liberi sono gli stati eccitati.
La
a energia più bassa verranno occupate da elettroni.
Gli stati che restano liberi sono gli stati eccitati.
La ![]() va pensata limitata agli stati occupati.
va pensata limitata agli stati occupati.