



Next: Metodo di Newton-Raphson
Up: Ricerca degli zeri
Previous: Ricerca degli zeri
Contents
Metodo di bisezione
Si inizia con un intervallo ![$[a,b]$](img977.gif) che include uno zero,
e uno solo, in modo che sia
che include uno zero,
e uno solo, in modo che sia 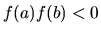 .
L'algoritmo di bisezione dimezza l'intervallo ad ogni iterazione,
raffinando sempre più la stima di
.
L'algoritmo di bisezione dimezza l'intervallo ad ogni iterazione,
raffinando sempre più la stima di 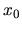 :
:
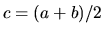
- se
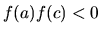 si ridefinisce
si ridefinisce 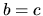 ; altrimenti
se
; altrimenti
se 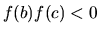 si ridefinisce
si ridefinisce 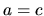 .
.
- si ottiene così un nuovo intervallo
![$[a,b]$](img977.gif) di ampiezza
dimezzata, su cui si ripete il procedimento.
di ampiezza
dimezzata, su cui si ripete il procedimento.
La convergenza è garantita (è impossibile "perdere" lo zero),
e il logaritmo dell'errore diminuisce linearmente col numero di
iterazioni. Possono sorgere difficoltà relativamente al criterio
di arresto. Ad esempio:
- Errore assoluto:
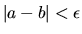 . Questo può dare problemi se
. Questo può dare problemi se 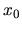 è molto grande: gli errori di arrotondamento in
è molto grande: gli errori di arrotondamento in 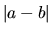 potrebbero essere più grandi di
potrebbero essere più grandi di 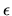 .
.
- Errore relativo:
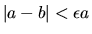 . Questo può dare problemi
in prossimità di
. Questo può dare problemi
in prossimità di 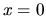 .
.
- Se la pendenza di
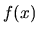 vicino allo zero è molto piccola,
potrebbe esserci un intero intervallo in cui
vicino allo zero è molto piccola,
potrebbe esserci un intero intervallo in cui 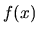 è indistinguibile
da zero nella rappresentazione della macchina.
è indistinguibile
da zero nella rappresentazione della macchina.
furio
2002-02-24
![]() che include uno zero,
e uno solo, in modo che sia
che include uno zero,
e uno solo, in modo che sia ![]() .
L'algoritmo di bisezione dimezza l'intervallo ad ogni iterazione,
raffinando sempre più la stima di
.
L'algoritmo di bisezione dimezza l'intervallo ad ogni iterazione,
raffinando sempre più la stima di ![]() :
: