



Next: Energia di punto zero
Up: L'oscillatore armonico
Previous: Unità
Contents
Come si può facilmente verificare, per grandi 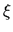 (tali da poter trascurare
(tali da poter trascurare 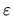 ) le soluzioni
della (2.14) devono avere l'andamento asintotico
) le soluzioni
della (2.14) devono avere l'andamento asintotico
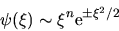 |
(2.15) |
dove 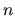 ha un qualsiasi valore finito.
Il segno + nell'esponente deve però essere scartato a priori
perchè darebbe luogo a soluzioni divergenti e quindi
non normalizzabili (inoltre, l'intuizione stessa ci dice
che la particella non dovrebbe tendere ad allontanarsi
da
ha un qualsiasi valore finito.
Il segno + nell'esponente deve però essere scartato a priori
perchè darebbe luogo a soluzioni divergenti e quindi
non normalizzabili (inoltre, l'intuizione stessa ci dice
che la particella non dovrebbe tendere ad allontanarsi
da 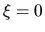 , punto verso cui è diretta la forza).
Sembra quindi conveniente provare a scorporare l'andamento
asintotico desiderato ponendo
, punto verso cui è diretta la forza).
Sembra quindi conveniente provare a scorporare l'andamento
asintotico desiderato ponendo
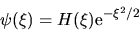 |
(2.16) |
dove  è una funzione che a grandi
è una funzione che a grandi 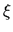 si deve
comportare in modo che l'andamento sia determinato
dal secondo fattore
si deve
comportare in modo che l'andamento sia determinato
dal secondo fattore
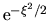 .
.  non deve,
in particolare, crescere come
non deve,
in particolare, crescere come
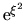 , altrimenti
saremmo in presenza di una delle soluzioni che non desideriamo.
, altrimenti
saremmo in presenza di una delle soluzioni che non desideriamo.
Con la posizione (2.16) la (2.14)
diventa, per la nuova funzione incognita  ,
,
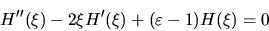 |
(2.17) |
Vediamo subito che
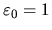 ,
, 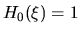 è la soluzione più semplice. Come tra poco si vedrà,
questa è la soluzione che rappresenta lo stato fondamentale,
cioè quello ad energia più bassa.
è la soluzione più semplice. Come tra poco si vedrà,
questa è la soluzione che rappresenta lo stato fondamentale,
cioè quello ad energia più bassa.
Per ottenere le soluzioni generali espandiamo  in una serie (in principio infinita):
in una serie (in principio infinita):
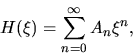 |
(2.18) |
deriviamo la serie per ottenere le derivate e riscriviamo la
(2.17) combinando i termini con la stessa potenza
di 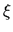 :
:
![\begin{displaymath}
\sum_{n=0}^\infty \left[
(n+2)(n+1) A_{n+2} + (\varepsilon-2n-1) A_n
\right] \xi^n = 0
\end{displaymath}](img90.gif) |
(2.19) |
Affinchè ciò sia soddisfatto per qualsiasi valore di 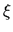 è necessario che tutti i coefficienti siano nulli:
è necessario che tutti i coefficienti siano nulli:
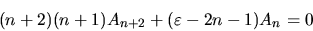 |
(2.20) |
Così, una volta dati 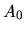 e
e 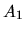 , la (2.20)
permette di determinare per ricursione l'intera soluzione
in forma di serie di potenze.
, la (2.20)
permette di determinare per ricursione l'intera soluzione
in forma di serie di potenze.
Supponiamo che la serie sia veramente una serie infinita.
A grandi 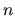 i termini si comportano quindi come
i termini si comportano quindi come
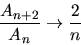 |
(2.21) |
Ma, ricordando che
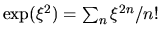 ,
i cui coefficienti soddisfano pure alla (2.21),
vediamo che questa relazione tra i coefficienti fa crescere
,
i cui coefficienti soddisfano pure alla (2.21),
vediamo che questa relazione tra i coefficienti fa crescere
 come
come 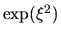 , ossia ci fornisce delle soluzioni
divergenti indesiderate.
L'unica maniera per evitare che questo accada è fare in modo
che, nella (2.20), tutti i coefficienti da un certo
punto in poi siano nulli, in modo che la serie si riduca in
realtà ad un polinomio di grado finito. Questo avviene
se e solo se
, ossia ci fornisce delle soluzioni
divergenti indesiderate.
L'unica maniera per evitare che questo accada è fare in modo
che, nella (2.20), tutti i coefficienti da un certo
punto in poi siano nulli, in modo che la serie si riduca in
realtà ad un polinomio di grado finito. Questo avviene
se e solo se
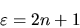 |
(2.22) |
dove 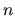 è un intero positivo o nullo.
è un intero positivo o nullo.
Corrispondentemente, le energie possibili per l'oscillatore
armonico sono quantizzate:
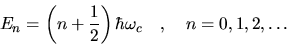 |
(2.23) |
I corrispondenti polinomi 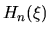 sono detti
polinomi di Hermite.
sono detti
polinomi di Hermite. 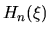 è di grado
è di grado 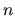 in
in 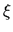 , ha
, ha 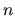 nodi, ed è pari [
nodi, ed è pari [
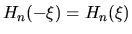 ] o dispari
[
] o dispari
[
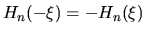 ] a seconda che
] a seconda che 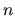 sia pari o dispari.
Poichè
sia pari o dispari.
Poichè
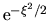 non ha nodi ed è pari,
anche l'intera autofunzione corrispondente all'autovalore
dell'energia
non ha nodi ed è pari,
anche l'intera autofunzione corrispondente all'autovalore
dell'energia 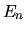
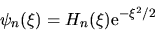 |
(2.24) |
ha 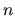 nodi e la parità di
nodi e la parità di 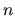 .
Più sotto si mostra come una parità definita è una conseguenza
della simmetria del problema rispetto all'inversione dell'asse
.
Più sotto si mostra come una parità definita è una conseguenza
della simmetria del problema rispetto all'inversione dell'asse 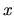 .
.
I polinomi di Hermite di ordine più basso sono
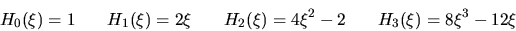 |
(2.25) |
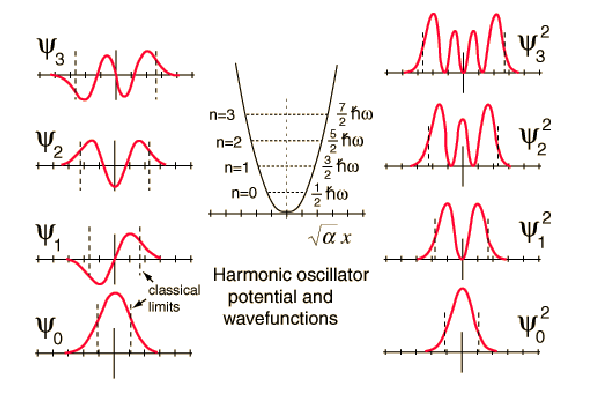
Un grafico delle corrispondenti funzioni d'onda e densità di
probabilità è riportato in fig. 2.1.
Figure 2.1:
Funzioni d'onda e densità di probabilità
dell'oscillatore armonico quantistico.
 |




Next: Energia di punto zero
Up: L'oscillatore armonico
Previous: Unità
Contents
furio
2002-02-24
![]() (tali da poter trascurare
(tali da poter trascurare ![]() ) le soluzioni
della (2.14) devono avere l'andamento asintotico
) le soluzioni
della (2.14) devono avere l'andamento asintotico
![]() ,
,
![]() in una serie (in principio infinita):
in una serie (in principio infinita):
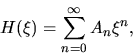
![\begin{displaymath}
\sum_{n=0}^\infty \left[
(n+2)(n+1) A_{n+2} + (\varepsilon-2n-1) A_n
\right] \xi^n = 0
\end{displaymath}](img90.gif)
![]() i termini si comportano quindi come
i termini si comportano quindi come