



Next: Valori medi
Up: Aspetti importanti della meccanica
Previous: Ortonormalità delle autofunzioni dell'hamiltoniano
Contents
La linearità dell'equazione di Schrödinger ci assicura che,
se 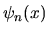 sono le autofunzioni dell'equazione indipendente
dal tempo, tutte le loro combinazioni lineari
sono le autofunzioni dell'equazione indipendente
dal tempo, tutte le loro combinazioni lineari
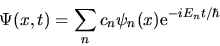 |
(3.31) |
sono anche una soluzione.
La (3.17) ci permette di dimostrare l'inverso,
ossia che una generica soluzione 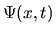 della
(2.3) può sempre essere espansa secondo la
(3.31).
della
(2.3) può sempre essere espansa secondo la
(3.31).
Per dimostrare ciò, consideriamo l'istante 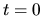 e poniamo
e poniamo
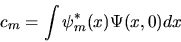 |
(3.32) |
e quindi consideriamo la funzione
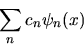 |
(3.33) |
Questa funzione è una soluzione (in quanto combinazione lineare
di soluzioni), e all'istante 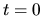 deve coincidere con
deve coincidere con 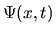 .
Infatti vale per ogni
.
Infatti vale per ogni 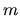 l'identità
l'identità
![\begin{displaymath}
c_m = \sum_n c_n \delta_{mn} =
\sum_n c_n \int \psi^*_m(x) \...
...) dx =
\int \psi^*_m(x) \left[ \sum_n c_n \psi_n(x) \right] dx
\end{displaymath}](img278.gif) |
(3.34) |
[si noti che abbiamo usato la (3.17)].
Questo è possibile solo se
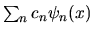 coincide
con
coincide
con 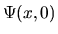 .
Ma dato il valore di una funzione d'onda ad un certo istante,
la sua evoluzione è completamente determinata dall'equazione
di Schrödinger temporale, e quindi l'evoluzione di
.
Ma dato il valore di una funzione d'onda ad un certo istante,
la sua evoluzione è completamente determinata dall'equazione
di Schrödinger temporale, e quindi l'evoluzione di 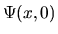 dovrà essere la stessa di
dovrà essere la stessa di
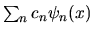 , cioè
quella indicata dalla (3.31).
, cioè
quella indicata dalla (3.31).




Next: Valori medi
Up: Aspetti importanti della meccanica
Previous: Ortonormalità delle autofunzioni dell'hamiltoniano
Contents
furio
2002-02-24
![]() sono le autofunzioni dell'equazione indipendente
dal tempo, tutte le loro combinazioni lineari
sono le autofunzioni dell'equazione indipendente
dal tempo, tutte le loro combinazioni lineari
![]() e poniamo
e poniamo
![\begin{displaymath}
c_m = \sum_n c_n \delta_{mn} =
\sum_n c_n \int \psi^*_m(x) \...
...) dx =
\int \psi^*_m(x) \left[ \sum_n c_n \psi_n(x) \right] dx
\end{displaymath}](img278.gif)