



Next: Definizione generale di momento
Up: Aspetti importanti della meccanica
Previous: Quantità conservate
Contents
Il momento angolare in un campo centrale
Immaginiamo di avere una particella in tre dimensioni immersa
in un campo centrale, ossia soggetta ad un potenziale 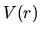 dipendente solo dalla distanza rispetto a un punto fisso.
In meccanica classica si definisce il momento angolare come
dipendente solo dalla distanza rispetto a un punto fisso.
In meccanica classica si definisce il momento angolare come
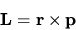 |
(3.85) |
dove 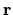 è il vettore posizione e
è il vettore posizione e 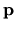 il vettore
impulso (quantità di moto). Risulta che
il vettore
impulso (quantità di moto). Risulta che 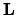 è una
quantità conservata, con importanti conseguenze tra cui la
planarità dell'orbita.
Ci aspettiamo che anche il corrispondente operatore quantistico
giochi un ruolo importante, ed infatti così è.
è una
quantità conservata, con importanti conseguenze tra cui la
planarità dell'orbita.
Ci aspettiamo che anche il corrispondente operatore quantistico
giochi un ruolo importante, ed infatti così è.
Possiamo immediatamente dire qualcosa sulle sue proprietà
di commutazione, facendo uso delle (3.67)--(3.70)
e utilizzando la proprietà generale (immediatamente dimostrata)
![\begin{displaymath}[AB,C]= A[B,C] + [A,C]B
\end{displaymath}](img383.gif) |
(3.86) |
Si trova
![\begin{displaymath}[L_x,x]= 0 ,
[L_x,y] = i\hbar z ,
[L_x,z] = -i\hbar y
\end{displaymath}](img384.gif) |
(3.87) |
e
![\begin{displaymath}[L_x,p_x]= 0 ,
[L_x,p_y] = i\hbar p_z ,
[L_x,p_z] = -i\hbar p_y
\end{displaymath}](img385.gif) |
(3.88) |
e proprietà analoghe ottenute ciclando gli indici per 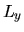 e
e 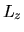 .
Si può far vedere che analoghe proprietà valgono per i
commutatori fra componenti di
.
Si può far vedere che analoghe proprietà valgono per i
commutatori fra componenti di 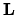 :
:
![\begin{displaymath}[L_x,L_x]= 0 ,
[L_x,L_y] = i\hbar L_z ,
[L_x,L_z] = -i\hbar L_y
\end{displaymath}](img388.gif) |
(3.89) |
e in realtà è vero per qualsiasi grandezza vettoriale 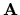 ,
funzione arbitraria di coordinate e impulsi:
,
funzione arbitraria di coordinate e impulsi:
![\begin{displaymath}[L_x,A_x]= 0 ,
[L_x,A_y] = i\hbar A_z ,
[L_x,A_z] = -i\hbar A_y
\end{displaymath}](img390.gif) |
(3.90) |
Inoltre, dati due vettori 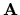 e
e 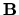 (sempre corrispondenti
ad operatori quantistici), si può costruire l'operatore
``prodotto scalare''
(sempre corrispondenti
ad operatori quantistici), si può costruire l'operatore
``prodotto scalare''
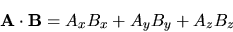 |
(3.91) |
e risulta
![\begin{displaymath}[L_x,{\bf A}\cdot{\bf B}]= [L_y,{\bf A}\cdot{\bf B}] =
[L_z,{\bf A}\cdot{\bf B}] = 0
\end{displaymath}](img393.gif) |
(3.92) |
come si dimostra subito usando le (3.90).
In particolare, facendo coincidere 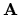 e
e 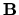 con
con
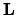 stesso, abbiamo anche
stesso, abbiamo anche
![\begin{displaymath}[L_x,L^2]= [L_y,L^2] = [L_z,L^2] = 0
\end{displaymath}](img396.gif) |
(3.93) |
Come si vedrà nella sezione 4.2, e come intuibile
dal risultato classico, per una particella in un campo centrale
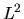 commuta con
commuta con 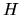 , ed è quindi una quantità conservata
che dà origine a un buon numero quantico.
Anche ogni singola componente di
, ed è quindi una quantità conservata
che dà origine a un buon numero quantico.
Anche ogni singola componente di 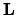 commuta con
commuta con 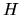 .
Però, le (3.89) mostrano che due diverse componenti
di
.
Però, le (3.89) mostrano che due diverse componenti
di 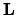 non commutano fra loro, e non sono pertanto
misurabili simultaneamente.
non commutano fra loro, e non sono pertanto
misurabili simultaneamente.
Esprimiamo il momento angolare nella rappresentazione delle
coordinate:
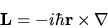 |
(3.94) |
Consideriamo un sistema di riferimento polare
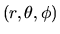 ,
dove l'asse polare coincide con l'asse cartesiano
,
dove l'asse polare coincide con l'asse cartesiano 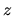 ,
,
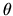 è l'angolo polare e
è l'angolo polare e 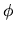 quello azimutale.
Siano
quello azimutale.
Siano 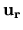 ,
, 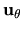 e
e 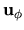 i versori
(che costituiscono una terna ortonormale destrorsa)
associati a spostamenti in cui varia solo
i versori
(che costituiscono una terna ortonormale destrorsa)
associati a spostamenti in cui varia solo 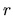 ,
, 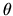 o
o
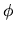 rispettivamente. Si ha
rispettivamente. Si ha
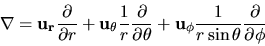 |
(3.95) |
Applicando la (3.94),
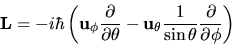 |
(3.96) |
Esprimendo i versori della terna polare in funzione di quelli
della terna cartesiana
possiamo calcolare le componenti cartesiane di 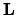 nello
spazio polare. In particolare risulta
nello
spazio polare. In particolare risulta
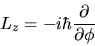 |
(3.100) |
e
![\begin{displaymath}
L^2 = -\hbar^2 \left[
\frac{1}{\sin\theta} \frac{\partial}{\...
...rac{1}{\sin^2\theta} \frac{\partial^2}{\partial\phi^2}
\right]
\end{displaymath}](img415.gif) |
(3.101) |
Cerchiamo ora le autofunzioni dell'operatore 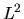 , che
torneranno utili in seguito risolvendo l'equazione di Schrödinger
per una particella in un campo centrale:
, che
torneranno utili in seguito risolvendo l'equazione di Schrödinger
per una particella in un campo centrale:
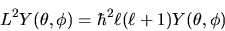 |
(3.102) |
dove abbiamo espresso in questo modo (per futura convenienza)
l'autovalore.
Notiamo che, moltiplicando i due membri per
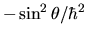 ,
l'equazione agli autovalori diventa
,
l'equazione agli autovalori diventa
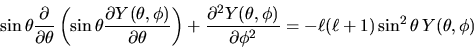 |
(3.103) |
Supponiamo che la soluzione sia separabile in una funzione di
solo 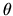 e una di solo
e una di solo 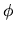 :
:
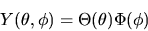 |
(3.104) |
e dividiamo il risultato per 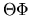 :
:
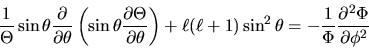 |
(3.105) |
Il primo membro è funzione solo di 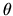 , e il secondo
solo di
, e il secondo
solo di 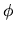 . Entrambi devono allora essere uguali a una
costante, che indichiamo con
. Entrambi devono allora essere uguali a una
costante, che indichiamo con 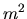 . Abbiamo allora ottenuto
due equazioni:
. Abbiamo allora ottenuto
due equazioni:
![\begin{displaymath}
\frac{1}{\sin\theta} \frac{d}{d\theta}
\left( \sin\theta \fr...
...t[ \ell(\ell+1) - \frac{m^2}{\sin^2\theta} \right]
\Theta = 0
\end{displaymath}](img423.gif) |
(3.106) |
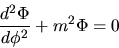 |
(3.107) |
La seconda ci dice che deve essere
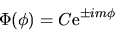 |
(3.108) |
Poichè 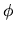 è un angolo azimutale, è necessario che
è un angolo azimutale, è necessario che 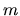 sia intero affinchè la funzione sia ad un solo valore.
sia intero affinchè la funzione sia ad un solo valore.
La (3.106), usando 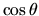 come variabile, è nota in
fisica matematica come equazione di Legendre. Si può risolvere in modo
analogo a quanto fatto per l'oscillatore armonico: esprimendo cioè la
soluzione in forma di una serie di potenze di
come variabile, è nota in
fisica matematica come equazione di Legendre. Si può risolvere in modo
analogo a quanto fatto per l'oscillatore armonico: esprimendo cioè la
soluzione in forma di una serie di potenze di 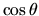 , e richiedendo
che non diverga per alcun valore di
, e richiedendo
che non diverga per alcun valore di 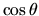 . Risulta che una
divergenza a
. Risulta che una
divergenza a 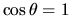 può essere evitata solo se si assume che la
serie sia in realtà un polinomio di grado finito, ossia che tutti i
coefficienti da un certo grado in poi siano nulli. Si può vedere che
questo implica
può essere evitata solo se si assume che la
serie sia in realtà un polinomio di grado finito, ossia che tutti i
coefficienti da un certo grado in poi siano nulli. Si può vedere che
questo implica 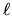 intero, e
intero, e 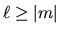 . Le funzioni risultanti sono
indicate con
. Le funzioni risultanti sono
indicate con
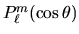 e si chiamano funzioni
associate ai polinomi di Legendre. I polinomi di Legendre
e si chiamano funzioni
associate ai polinomi di Legendre. I polinomi di Legendre
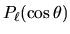 sono le soluzioni dell'equazione di Legendre
per
sono le soluzioni dell'equazione di Legendre
per 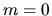 , e le funzioni associate sono ad essi connesse da
, e le funzioni associate sono ad essi connesse da
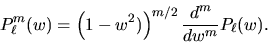 |
(3.109) |
Le autofunzioni dell'operatore 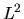 hanno dunque la forma
hanno dunque la forma
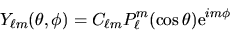 |
(3.110) |
dove 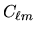 è una costante di normalizzazione,
e sono dette armoniche sferiche.
Poiche
è una costante di normalizzazione,
e sono dette armoniche sferiche.
Poiche 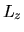 , dato dalla (3.100), opera solo su
, dato dalla (3.100), opera solo su 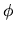 ,
queste sono anche autofunzioni di questo operatore:
,
queste sono anche autofunzioni di questo operatore:
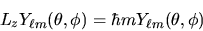 |
(3.111) |
In sostanza,
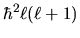 rappresenta il modulo quadrato
del momento angolare, e
rappresenta il modulo quadrato
del momento angolare, e 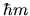 la sua proiezione lungo l'asse
la sua proiezione lungo l'asse 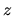 .
.
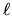 dev'essere un intero positivo o nullo, e
dev'essere un intero positivo o nullo, e 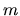 un intero
compreso fra
un intero
compreso fra 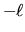 e
e 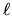 . Per un dato
. Per un dato 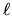 ci sono dunque
ci sono dunque
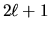 valori permessi per
valori permessi per 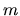 .
.




Next: Definizione generale di momento
Up: Aspetti importanti della meccanica
Previous: Quantità conservate
Contents
furio
2002-02-24
![]() dipendente solo dalla distanza rispetto a un punto fisso.
In meccanica classica si definisce il momento angolare come
dipendente solo dalla distanza rispetto a un punto fisso.
In meccanica classica si definisce il momento angolare come
![]() commuta con
commuta con ![]() , ed è quindi una quantità conservata
che dà origine a un buon numero quantico.
Anche ogni singola componente di
, ed è quindi una quantità conservata
che dà origine a un buon numero quantico.
Anche ogni singola componente di ![]() commuta con
commuta con ![]() .
Però, le (3.89) mostrano che due diverse componenti
di
.
Però, le (3.89) mostrano che due diverse componenti
di ![]() non commutano fra loro, e non sono pertanto
misurabili simultaneamente.
non commutano fra loro, e non sono pertanto
misurabili simultaneamente.
![]() , che
torneranno utili in seguito risolvendo l'equazione di Schrödinger
per una particella in un campo centrale:
, che
torneranno utili in seguito risolvendo l'equazione di Schrödinger
per una particella in un campo centrale:
![]() come variabile, è nota in
fisica matematica come equazione di Legendre. Si può risolvere in modo
analogo a quanto fatto per l'oscillatore armonico: esprimendo cioè la
soluzione in forma di una serie di potenze di
come variabile, è nota in
fisica matematica come equazione di Legendre. Si può risolvere in modo
analogo a quanto fatto per l'oscillatore armonico: esprimendo cioè la
soluzione in forma di una serie di potenze di ![]() , e richiedendo
che non diverga per alcun valore di
, e richiedendo
che non diverga per alcun valore di ![]() . Risulta che una
divergenza a
. Risulta che una
divergenza a ![]() può essere evitata solo se si assume che la
serie sia in realtà un polinomio di grado finito, ossia che tutti i
coefficienti da un certo grado in poi siano nulli. Si può vedere che
questo implica
può essere evitata solo se si assume che la
serie sia in realtà un polinomio di grado finito, ossia che tutti i
coefficienti da un certo grado in poi siano nulli. Si può vedere che
questo implica ![]() intero, e
intero, e ![]() . Le funzioni risultanti sono
indicate con
. Le funzioni risultanti sono
indicate con
![]() e si chiamano funzioni
associate ai polinomi di Legendre. I polinomi di Legendre
e si chiamano funzioni
associate ai polinomi di Legendre. I polinomi di Legendre
![]() sono le soluzioni dell'equazione di Legendre
per
sono le soluzioni dell'equazione di Legendre
per ![]() , e le funzioni associate sono ad essi connesse da
, e le funzioni associate sono ad essi connesse da
![]() hanno dunque la forma
hanno dunque la forma
![]() rappresenta il modulo quadrato
del momento angolare, e
rappresenta il modulo quadrato
del momento angolare, e ![]() la sua proiezione lungo l'asse
la sua proiezione lungo l'asse ![]() .
.
![]() dev'essere un intero positivo o nullo, e
dev'essere un intero positivo o nullo, e ![]() un intero
compreso fra
un intero
compreso fra ![]() e
e ![]() . Per un dato
. Per un dato ![]() ci sono dunque
ci sono dunque
![]() valori permessi per
valori permessi per ![]() .
.