- ... sinistra2.1
-
Si noti lo statement y(mesh) = dx: ha il solo scopo
di forzare il segno della soluzione ad essere positivo,
in quanto la parte ottenuta a sinistra del punto di raccordo
è pure positiva. Il valore
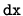 non ha particolare
importanza, dal momento che in seguito la soluzione viene riscalata
per raccordarsi con l'altra in modo continuo alla giunzione.
non ha particolare
importanza, dal momento che in seguito la soluzione viene riscalata
per raccordarsi con l'altra in modo continuo alla giunzione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... osservare2.2
-
Un suggerimento: è utile graficare assieme alle autofunzioni o alle
densità di probabilità anche la densità di probabilità classica
nella quarta colonna, che indica la posizione dei punti di inversione
classici. Con gnuplot questo si ottiene aggiungendo in coda
al comando plot:
,"
filename" using 1:4 with lines
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ortogonalità3.1
-
La condizione di ortogonalità fra due vettori ordinari,
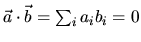 è analoga alla
(3.17) qualora si consideri l'integrale
come una ``somma su tutti gli
è analoga alla
(3.17) qualora si consideri l'integrale
come una ``somma su tutti gli 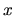 '', e che la coniugazione
complessa del primo termine è necessaria per far sì
che il prodotto scalare di un oggetto con se stesso sia
una misura della sua ``norma''.
'', e che la coniugazione
complessa del primo termine è necessaria per far sì
che il prodotto scalare di un oggetto con se stesso sia
una misura della sua ``norma''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complessiva4.1
-
Come si vedrà in seguito, in realtà c'è ancora un
fattore 2 dovuto allo spin.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fornisce5.1
-
Lo scettico può separare i coefficienti in una parte reale
e una immaginaria
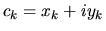 , richiedere che siano
nulle sia le derivate rispetto a
, richiedere che siano
nulle sia le derivate rispetto a 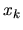 che quelle rispetto
a
che quelle rispetto
a 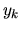 , e otterrà (sfruttando l'hermiticità) un sistema
, e otterrà (sfruttando l'hermiticità) un sistema
dove
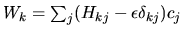 , che
ammette come soluzione solo
, che
ammette come soluzione solo 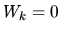 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.