



Next: Sviluppo in funzioni non
Up: Problema secolare
Previous: Problema secolare
Contents
Supponiamo di avere a disposizione una base di 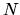 funzioni
funzioni
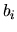 fra loro ortonormali:
fra loro ortonormali:
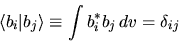 |
(5.64) |
ed espandiamo una generica 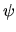 in questa base:
in questa base:
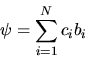 |
(5.65) |
Sostituendo la (5.65) nella (5.63) si vede
immediatamente che quest'ultima prende la forma
dove si è posto
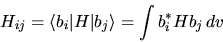 |
(5.67) |
Poichè sia 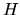 che la base sono dati,
che la base sono dati, 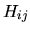 è una matrice
quadrata di numeri perfettamente nota, e che per la proprietà
di hermiticità dell'operatore hamiltoniano tale che
è una matrice
quadrata di numeri perfettamente nota, e che per la proprietà
di hermiticità dell'operatore hamiltoniano tale che
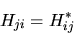 |
(5.68) |
(quindi simmetrica nel caso in cui tutti gli elementi siano reali).
Come richiesto dal metodo variazionale, minimizziamo la
(5.66) rispetto ai coefficienti:
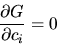 |
(5.69) |
e questo fornisce5.1
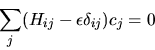 |
(5.70) |
Notiamo che se la base fosse un sistema completo (e quindi
infinita), questa sarebbe una forma dell'equazione di Schrödinger.
Abbiamo quindi dimostrato che queste stesse equazioni, nel
caso in cui la base sia finita, costituiscono la migliore
approssimazione possibile alla vera soluzione secondo
il principio variazionale.
La (5.70) è un sistema di 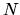 equazioni algebriche
lineari e omogenee (non ci sono termini costanti) per le
equazioni algebriche
lineari e omogenee (non ci sono termini costanti) per le 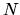 incognite
incognite 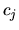 . In generale questo sistema ha come unica
soluzione possibile tutti i
. In generale questo sistema ha come unica
soluzione possibile tutti i 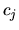 nulli (caso che ovviamente
non corrisponde ad alcuna funzione d'onda).
Per avere soluzioni non nulle è necessario che il determinante
dei coefficienti sia nullo:
nulli (caso che ovviamente
non corrisponde ad alcuna funzione d'onda).
Per avere soluzioni non nulle è necessario che il determinante
dei coefficienti sia nullo:
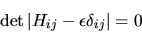 |
(5.71) |
Ciò corrisponde in pratica a dire che una delle equazioni
è una combinazione lineare delle altre, e quindi il
sistema si riduce in realtà a un sistema di 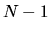 equazioni
con
equazioni
con 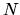 incognite, che ammette soluzione non nulla.
incognite, che ammette soluzione non nulla.
La (5.71) è detta equazione secolare.
Si tratta di una equazione algebrica di grado 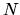 in
in 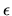 (come subito si vede espandendo il determinante e notando che
la diagonale principale genera un termine contenente
(come subito si vede espandendo il determinante e notando che
la diagonale principale genera un termine contenente 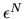 ,
e tutte le altre diagonali termini con potenze inferiori),
che possiede quindi
,
e tutte le altre diagonali termini con potenze inferiori),
che possiede quindi 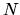 radici.
Queste radici sono dette gli autovalori.
La (5.70) può anche essere scritta in forma matriciale
radici.
Queste radici sono dette gli autovalori.
La (5.70) può anche essere scritta in forma matriciale
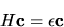 |
(5.72) |
dove 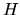 è qui la matrice
è qui la matrice 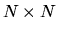 costituita dagli
costituita dagli 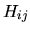 ,
e
,
e 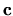 è un vettore costituito dai
è un vettore costituito dai 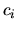 disposti in colonna.
Le soluzioni
disposti in colonna.
Le soluzioni 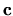 sono quindi anche chiamati autovettori.
Per ogni radice (autovalore) vi sarà un corrispondente
autovettore (determinato a meno di una costante moltiplicativa,
fissata dalla normalizzazione). Avremo quindi
sono quindi anche chiamati autovettori.
Per ogni radice (autovalore) vi sarà un corrispondente
autovettore (determinato a meno di una costante moltiplicativa,
fissata dalla normalizzazione). Avremo quindi 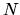 autovettori.
Si potrà allora scrivere che vi sono
autovettori.
Si potrà allora scrivere che vi sono 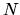 soluzioni
soluzioni
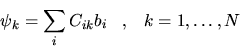 |
(5.73) |
dove 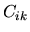 è una matrice costruita disponendo in colonna,
fianco a fianco, gli
è una matrice costruita disponendo in colonna,
fianco a fianco, gli 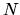 autovettori, e tali che
autovettori, e tali che
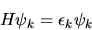 |
(5.74) |
ovvero, in forma matriciale, prendendo la componente 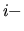 ima,
ima,
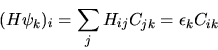 |
(5.75) |
La (5.72) è una equazione comune nell'algebra
lineare, ed esistono metodi standard per risolverla.
Data una matrice 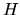 , si ottengono quindi facilmente--attraverso
routine di libreria--la matrice
, si ottengono quindi facilmente--attraverso
routine di libreria--la matrice 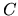 e un vettore di autovalori
e un vettore di autovalori
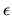 .
.
Il processo di risoluzione è anche noto come diagonalizzazione.
Questo nome deriva dalla seguente importante proprietà di 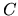 .
La (5.73) può essere vista come una trasformazione
delle
.
La (5.73) può essere vista come una trasformazione
delle 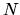 funzioni di partenza in un altro insieme di
funzioni di partenza in un altro insieme di 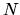 funzioni
attraverso una matrice di trasformazione. Si può far vedere
che se le
funzioni
attraverso una matrice di trasformazione. Si può far vedere
che se le 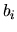 sono fra loro ortonormali anche le
sono fra loro ortonormali anche le 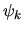 lo sono.
Si dice allora che la trasformazione è unitaria.
Ciò corrisponde ad affermare che
lo sono.
Si dice allora che la trasformazione è unitaria.
Ciò corrisponde ad affermare che
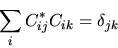 |
(5.76) |
o in notazione matriciale
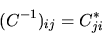 |
(5.77) |
ossia la matrice inversa è uguale alla trasposta coniugata.
Consideriamo ora il prodotto di matrici 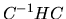 e calcoliamo
un suo elemento:
e calcoliamo
un suo elemento:
avendo fatto uso dei risultati precedenti.
Si dice allora che la trasformazione 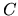 riduce
riduce 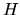 in forma
di una matrice diagonale, i cui
in forma
di una matrice diagonale, i cui 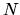 elementi non nulli
sono gli autovalori. Possiamo vedere quindi il nostro problema
agli autovalori come quello della ricerca di una trasformazione
che porti dalla base originale ad una nuova base in cui
l'operatore
elementi non nulli
sono gli autovalori. Possiamo vedere quindi il nostro problema
agli autovalori come quello della ricerca di una trasformazione
che porti dalla base originale ad una nuova base in cui
l'operatore 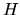 ha una forma diagonale, ossia agisce sugli
elementi della base semplicemente moltiplicandoli per una
costante (equazione di Schrödinger).
ha una forma diagonale, ossia agisce sugli
elementi della base semplicemente moltiplicandoli per una
costante (equazione di Schrödinger).




Next: Sviluppo in funzioni non
Up: Problema secolare
Previous: Problema secolare
Contents
furio
2002-02-24
![]() funzioni
funzioni
![]() fra loro ortonormali:
fra loro ortonormali:
![]() equazioni algebriche
lineari e omogenee (non ci sono termini costanti) per le
equazioni algebriche
lineari e omogenee (non ci sono termini costanti) per le ![]() incognite
incognite ![]() . In generale questo sistema ha come unica
soluzione possibile tutti i
. In generale questo sistema ha come unica
soluzione possibile tutti i ![]() nulli (caso che ovviamente
non corrisponde ad alcuna funzione d'onda).
Per avere soluzioni non nulle è necessario che il determinante
dei coefficienti sia nullo:
nulli (caso che ovviamente
non corrisponde ad alcuna funzione d'onda).
Per avere soluzioni non nulle è necessario che il determinante
dei coefficienti sia nullo:
![]() in
in ![]() (come subito si vede espandendo il determinante e notando che
la diagonale principale genera un termine contenente
(come subito si vede espandendo il determinante e notando che
la diagonale principale genera un termine contenente ![]() ,
e tutte le altre diagonali termini con potenze inferiori),
che possiede quindi
,
e tutte le altre diagonali termini con potenze inferiori),
che possiede quindi ![]() radici.
Queste radici sono dette gli autovalori.
La (5.70) può anche essere scritta in forma matriciale
radici.
Queste radici sono dette gli autovalori.
La (5.70) può anche essere scritta in forma matriciale
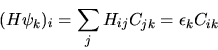
![]() , si ottengono quindi facilmente--attraverso
routine di libreria--la matrice
, si ottengono quindi facilmente--attraverso
routine di libreria--la matrice ![]() e un vettore di autovalori
e un vettore di autovalori
![]() .
.
![]() .
La (5.73) può essere vista come una trasformazione
delle
.
La (5.73) può essere vista come una trasformazione
delle ![]() funzioni di partenza in un altro insieme di
funzioni di partenza in un altro insieme di ![]() funzioni
attraverso una matrice di trasformazione. Si può far vedere
che se le
funzioni
attraverso una matrice di trasformazione. Si può far vedere
che se le ![]() sono fra loro ortonormali anche le
sono fra loro ortonormali anche le ![]() lo sono.
Si dice allora che la trasformazione è unitaria.
Ciò corrisponde ad affermare che
lo sono.
Si dice allora che la trasformazione è unitaria.
Ciò corrisponde ad affermare che
![]() e calcoliamo
un suo elemento:
e calcoliamo
un suo elemento: