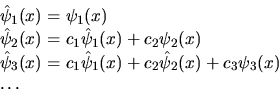Next: Sviluppo di una soluzione
Up: Aspetti importanti della meccanica
Previous: Pacchetti d'onda
Contents
Ortonormalità delle autofunzioni dell'hamiltoniano
Si dice che un insieme di funzioni d'onda complesse
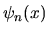 sono fra loro ortonormali se
sono fra loro ortonormali se
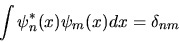 |
(3.17) |
Nel caso 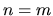 questo esprime semplicemente la normalizzazione
a 1 di una funzione d'onda, mentre nel caso
questo esprime semplicemente la normalizzazione
a 1 di una funzione d'onda, mentre nel caso 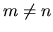 esprime
una condizione di ortogonalità3.1 fra le due funzioni.
esprime
una condizione di ortogonalità3.1 fra le due funzioni.
Dato l'operatore hamiltoniano
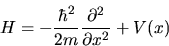 |
(3.18) |
le cui autofunzioni sono gli autostati dell'energia
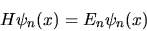 |
(3.19) |
vogliamo ora far vedere che
le 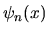 sono fra loro ortonormali, ossia
soddisfano alla (3.17).
sono fra loro ortonormali, ossia
soddisfano alla (3.17).
Per dimostrarlo, si consideri le due equazioni
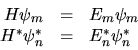 |
(3.20) |
Si moltiplichi a sinistra la prima per 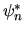 e la seconda
per
e la seconda
per 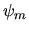 e si integri:
e si integri:
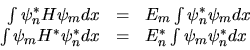 |
(3.21) |
Gli integrali nei membri a destra sono identici.
Facciamo ora vedere che i membri a sinistra devono essere uguali
fra loro (questo corrisponde a dimostrare l'hermiticità
dell'operatore 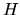 ).
L'identità è palese per quanto riguarda la parte di
).
L'identità è palese per quanto riguarda la parte di 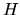 relativa al potenziale,
perchè
relativa al potenziale,
perchè 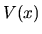 è un semplice fattore moltiplicativo reale.
Concentriamoci allora sul termine cinetico ed effettuiamo una
integrazione per parti:
è un semplice fattore moltiplicativo reale.
Concentriamoci allora sul termine cinetico ed effettuiamo una
integrazione per parti:
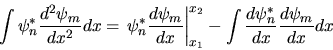 |
(3.22) |
e analogamente
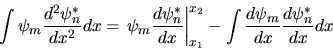 |
(3.23) |
Assumiamo che agli estremi di integrazione 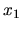 e
e 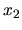 la funzione d'onda e le sue derivate sia nulla (se
così non fosse, si immagini di racchiudere l'intero
sistema, per quanto grande sia, in una scatola limitata
da barriere infinite, e di far corrispondere gli estremi
di integrazione con queste barriere).
Se i termini integrati sono nulli, abbiamo trovato che
la funzione d'onda e le sue derivate sia nulla (se
così non fosse, si immagini di racchiudere l'intero
sistema, per quanto grande sia, in una scatola limitata
da barriere infinite, e di far corrispondere gli estremi
di integrazione con queste barriere).
Se i termini integrati sono nulli, abbiamo trovato che
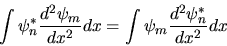 |
(3.24) |
e quindi che
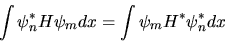 |
(3.25) |
La (3.21) ci dà allora
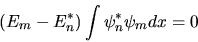 |
(3.26) |
Quando 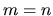 , l'integrale è 1, e quindi deve essere
, l'integrale è 1, e quindi deve essere
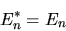 |
(3.27) |
ossia gli autovalori dell'energia sono senz'altro reali.
Supponiamo che sia 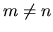 .
Se anche
.
Se anche 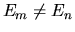 , allora deve essere
, allora deve essere
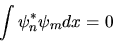 |
(3.28) |
ossia autofunzioni corrispondenti ad autovalori diversi sono
sicuramente ortogonali fra loro.
Può però anche accadere che sia 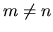 ma
ma
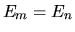 : è il caso della degenerazione.
: è il caso della degenerazione.
In questo caso la (3.28) potrebbe non essere
soddisfatta, ma si possono sempre scegliere le autofunzioni in
modo che lo sia. Supponiamo ad esempio che le prime 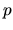 autofunzioni
autofunzioni
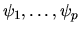 appartengano allo stesso
autovalore
appartengano allo stesso
autovalore 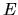 e siano linearmente indipendenti (ossia nessuna
di esse può essere espressa come combinazione lineare delle
altre), ma non siano fra loro ortogonali.
Ogni loro combinazione lineare è quindi anch'essa una
soluzione appartenente allo stesso autovalore
e siano linearmente indipendenti (ossia nessuna
di esse può essere espressa come combinazione lineare delle
altre), ma non siano fra loro ortogonali.
Ogni loro combinazione lineare è quindi anch'essa una
soluzione appartenente allo stesso autovalore 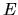 .
A partire dalle
.
A partire dalle
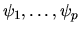 possiamo allora costruire
un nuovo insieme di autofunzioni del tutto equivalente
possiamo allora costruire
un nuovo insieme di autofunzioni del tutto equivalente
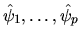 ,
in cui le autofunzioni sono ortogonali fra loro.
Si può ad esempio procedere in questo modo:
,
in cui le autofunzioni sono ortogonali fra loro.
Si può ad esempio procedere in questo modo:
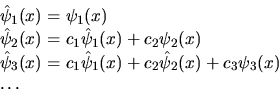 |
(3.29) |
dove 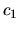 e
e 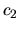 sono determinati da
sono determinati da
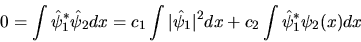 |
(3.30) |
e dalla condizione di normalizzazione, e così via
(si tratta del metodo di ortonormalizzazione di Schmidt).
Possiamo perciò interpretare la (3.28)
nel senso che se gli autovalori delle due autofunzioni sono
diversi esse devono essere ortogonali, mentre se sono
uguali esse possono essere scelte in modo da essere
ortogonali.




Next: Sviluppo di una soluzione
Up: Aspetti importanti della meccanica
Previous: Pacchetti d'onda
Contents
furio
2002-02-24
![]() sono fra loro ortonormali se
sono fra loro ortonormali se
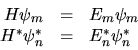
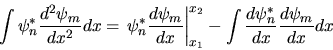
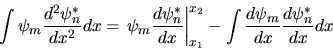
![]() autofunzioni
autofunzioni
![]() appartengano allo stesso
autovalore
appartengano allo stesso
autovalore ![]() e siano linearmente indipendenti (ossia nessuna
di esse può essere espressa come combinazione lineare delle
altre), ma non siano fra loro ortogonali.
Ogni loro combinazione lineare è quindi anch'essa una
soluzione appartenente allo stesso autovalore
e siano linearmente indipendenti (ossia nessuna
di esse può essere espressa come combinazione lineare delle
altre), ma non siano fra loro ortogonali.
Ogni loro combinazione lineare è quindi anch'essa una
soluzione appartenente allo stesso autovalore ![]() .
A partire dalle
.
A partire dalle
![]() possiamo allora costruire
un nuovo insieme di autofunzioni del tutto equivalente
possiamo allora costruire
un nuovo insieme di autofunzioni del tutto equivalente
![]() ,
in cui le autofunzioni sono ortogonali fra loro.
Si può ad esempio procedere in questo modo:
,
in cui le autofunzioni sono ortogonali fra loro.
Si può ad esempio procedere in questo modo: