



Next: Soluzione e livelli energetici
Up: L'oscillatore armonico
Previous: L'oscillatore armonico
Contents
L'equazione di Schrödinger di un oscillatore armonico
unidimensionale è [utilizzando una notazione simile
alla (2.2)]
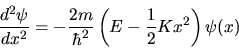 |
(2.11) |
dove 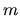 è la massa e
è la massa e 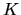 la costante di forza (la forza
a cui è soggetta la massa è cioè
la costante di forza (la forza
a cui è soggetta la massa è cioè 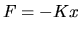 , proporzionale
allo spostamento e diretta verso l'origine).
Classicamente a un tale oscillatore corrisponde una frequenza
(angolare)
, proporzionale
allo spostamento e diretta verso l'origine).
Classicamente a un tale oscillatore corrisponde una frequenza
(angolare)
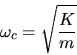 |
(2.12) |
È conveniente passare ad unità adimensionali (in cui
lavora il programma presentato in seguito). Si può porre
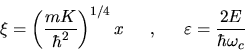 |
(2.13) |
[usando la definizione (2.12) per 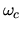 ]
ottenendo l'equazione equivalente
]
ottenendo l'equazione equivalente
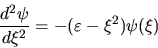 |
(2.14) |
che è espressa in unità adimensionali.
furio
2002-02-24