



Next: Quantità conservate
Up: Aspetti importanti della meccanica
Previous: La formulazione matriciale
Contents
Il valore medio del prodotto di operatori dipende dall'ordine
in cui gli operatori vengono applicati.
Prendiamo ad esempio una coordinata 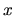 e il momento ad essa
coniugato
e il momento ad essa
coniugato 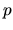 , e calcoliamo il valor medio del prodotto
, e calcoliamo il valor medio del prodotto 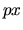 nella rappresentazione delle coordinate:
nella rappresentazione delle coordinate:
ovvero
![\begin{displaymath}
\langle xp - px \rangle = \langle [x,p] \rangle = i\hbar
\end{displaymath}](img337.gif) |
(3.66) |
dove con la notazione ![$[A,B]$](img338.gif) indichiamo l'operatore
indichiamo l'operatore 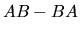 che chiameremo commutatore tra
che chiameremo commutatore tra 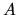 e
e 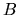 .
Diremo che
.
Diremo che 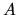 e
e 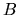 commutano quando il loro commutatore
è nullo, ossia quando è indifferente l'ordine con cui sono
applicati su uno stato. Come abbiamo appena visto questo non
è sempre vero.
commutano quando il loro commutatore
è nullo, ossia quando è indifferente l'ordine con cui sono
applicati su uno stato. Come abbiamo appena visto questo non
è sempre vero.
Il risultato (3.66) non dipende dallo stato, ed è quindi
una identità a livello di operatore:
![\begin{displaymath}[x,p_x]= i\hbar
\end{displaymath}](img342.gif) |
(3.67) |
(dove si è aggiunto l'indice 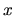 in
in 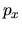 per sottolineare che
si tratta dell'impulso coniugato a
per sottolineare che
si tratta dell'impulso coniugato a 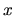 ).
Si può far vedere che le variabili come
).
Si può far vedere che le variabili come 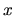 e
e 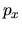 che
non commutano sono quelle non misurabili simultaneamente.
Invece,
che
non commutano sono quelle non misurabili simultaneamente.
Invece,
![\begin{displaymath}[x,y]=0
\end{displaymath}](img344.gif) |
(3.68) |
(non vi sono vincoli alla determinazione
simultanea di diverse coordinate di posizione),
![\begin{displaymath}[p_x,p_y]=0
\end{displaymath}](img345.gif) |
(3.69) |
(lo stesso per gli impulsi), e
![\begin{displaymath}[x,p_y]=0
\end{displaymath}](img346.gif) |
(3.70) |
(lo stesso per la coordinata in una direzione e
l'impulso in un'altra).
In generale, date due quantità osservabili 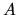 e
e 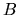 rappresentate in meccanica quantistica da operatori,
rappresentate in meccanica quantistica da operatori,
![$\vert\langle [A,B]\rangle \vert$](img347.gif) rappresenta il limite
inferiore al prodotto
rappresenta il limite
inferiore al prodotto
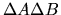 , dove
, dove
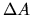 e
e 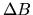 sono gli scarti quadratici medi
di misure effettuate simultaneamente su queste due variabili.
Si tratta di una versione più generale del principio di
indeterminazione. Se
sono gli scarti quadratici medi
di misure effettuate simultaneamente su queste due variabili.
Si tratta di una versione più generale del principio di
indeterminazione. Se 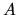 e
e 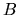 non commutano, è
impossibile determinarle entrambe simultaneamente con
precisione assoluta.
non commutano, è
impossibile determinarle entrambe simultaneamente con
precisione assoluta.
D'altra parte, si può vedere che se 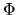 è un
autostato comune di
è un
autostato comune di 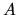 e
e 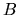 :
:
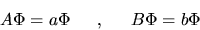 |
(3.71) |
(dove 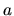 e
e 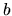 sono gli autovalori, ossia dei semplici numeri) allora
sono gli autovalori, ossia dei semplici numeri) allora
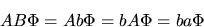 |
(3.72) |
e
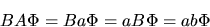 |
(3.73) |
sono uguali, ossia ![$[A,B]\Phi=0$](img357.gif) .
Se questo è vero per un insieme completo di autostati
(ad esempio, per tutte le autofunzioni dell'energia
.
Se questo è vero per un insieme completo di autostati
(ad esempio, per tutte le autofunzioni dell'energia 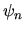 ),
allora ne segue necessariamente
),
allora ne segue necessariamente ![$[A,B]=0$](img358.gif) . Si può dimostrare
che è vero anche l'inverso: se
. Si può dimostrare
che è vero anche l'inverso: se 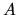 e
e 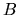 commutano, allora
hanno un insieme completo di autostati in comune.
commutano, allora
hanno un insieme completo di autostati in comune.




Next: Quantità conservate
Up: Aspetti importanti della meccanica
Previous: La formulazione matriciale
Contents
furio
2002-02-24
![]() e il momento ad essa
coniugato
e il momento ad essa
coniugato ![]() , e calcoliamo il valor medio del prodotto
, e calcoliamo il valor medio del prodotto ![]() nella rappresentazione delle coordinate:
nella rappresentazione delle coordinate:
![$\displaystyle \int \Psi^* \left[ -i\hbar \frac{\partial}{\partial x} (x\Psi) \right] dx$](img334.gif)
![$\displaystyle -i\hbar \int \Psi^*
\left[ \Psi + x \frac{\partial\Psi}{\partial x} \right] dx$](img335.gif)
![]() e
e ![]() rappresentate in meccanica quantistica da operatori,
rappresentate in meccanica quantistica da operatori,
![]() rappresenta il limite
inferiore al prodotto
rappresenta il limite
inferiore al prodotto
![]() , dove
, dove
![]() e
e ![]() sono gli scarti quadratici medi
di misure effettuate simultaneamente su queste due variabili.
Si tratta di una versione più generale del principio di
indeterminazione. Se
sono gli scarti quadratici medi
di misure effettuate simultaneamente su queste due variabili.
Si tratta di una versione più generale del principio di
indeterminazione. Se ![]() e
e ![]() non commutano, è
impossibile determinarle entrambe simultaneamente con
precisione assoluta.
non commutano, è
impossibile determinarle entrambe simultaneamente con
precisione assoluta.
![]() è un
autostato comune di
è un
autostato comune di ![]() e
e ![]() :
: