



Next: Il momento angolare in
Up: Aspetti importanti della meccanica
Previous: Regole di commutazione
Contents
Vogliamo ora dimostrare che dato un operatore 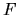 , e definito
l'operatore
, e definito
l'operatore 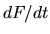 in modo tale che per ogni stato dipendente
dal tempo
in modo tale che per ogni stato dipendente
dal tempo 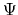 si abbia
si abbia
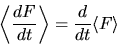 |
(3.74) |
ossia il valor medio di 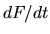 sullo stato sia pari alla
derivata temporale del valor medio di
sullo stato sia pari alla
derivata temporale del valor medio di 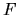 sullo stesso stato,
allora vale la importante relazione
sullo stesso stato,
allora vale la importante relazione
![\begin{displaymath}
i\hbar \frac{dF}{dt} = [F,H]
\end{displaymath}](img361.gif) |
(3.75) |
Questa relazione ci permette di identificare facilmente le
quantità conservate, che cioè non variano nel tempo:
sono quelle che commutano con l'hamiltoniano.
Per dimostrarlo, consideriamo la (3.47) per
il valor medio di 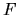 su uno stato
su uno stato 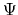 espanso in termini
di autofunzioni dell'energia, e deriviamola rispetto al tempo,
ottenendo così
espanso in termini
di autofunzioni dell'energia, e deriviamola rispetto al tempo,
ottenendo così
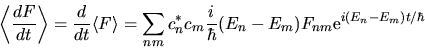 |
(3.76) |
Questo ci consente di identificare gli elementi di matrice
dell'operatore 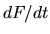 :
:
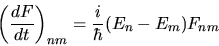 |
(3.77) |
(questo fa sì che la (3.47) valga
anche per questo operatore, come deve essere!).
Costruiamo ora invece l'elemento di matrice dell'operatore
![$[F,H]$](img364.gif) :
:
![$\displaystyle [F,H]_{nm}$](img365.gif) |
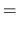 |
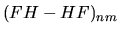 |
(3.78) |
| |
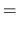 |
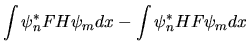 |
(3.79) |
| |
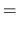 |
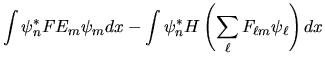 |
(3.80) |
| |
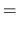 |
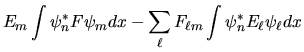 |
(3.81) |
| |
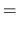 |
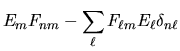 |
(3.82) |
| |
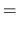 |
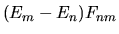 |
(3.83) |
Confrontando la (3.77) con la (3.83) vediamo che
![\begin{displaymath}
i\hbar \left( \frac{dF}{dt} \right)_{nm} = [F,H]_{nm}
\end{displaymath}](img372.gif) |
(3.84) |
Ma se questo vale per tutti gli elementi di matrice, l'uguaglianza
deve avvenire a livello di operatore, ossia la
(3.75) deve essere vera.
Siamo ora in posizione di comprendere cosa dobbiamo fare per
classificare in un modo utile gli stati di un sistema quantistico.
- La prima cosa da fare è cercare gli autovalori
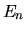 dell'hamiltoniana
dell'hamiltoniana 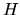 . Questo ci fornisce dei numeri
quantici
. Questo ci fornisce dei numeri
quantici 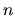 utili ai fini della classificazione. Sappiamo
che gli autostati di
utili ai fini della classificazione. Sappiamo
che gli autostati di 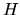 sono stazionari [vedere
(2.8)], quindi questi numeri quantici non
variano nel tempo: sono buoni numeri quantici.
sono stazionari [vedere
(2.8)], quindi questi numeri quantici non
variano nel tempo: sono buoni numeri quantici.
- Possono però esserci delle degenerazioni: ad un certo
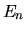 possono corrispondere diversi stati. Questi stati
differiranno per altri numeri quantici, che vorrei
saper determinare.
possono corrispondere diversi stati. Questi stati
differiranno per altri numeri quantici, che vorrei
saper determinare.
- Devo allora cercare un altro operatore
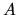 che commuti con
che commuti con 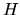 :
:
![$[A,H]=0$](img373.gif) . Questo garantisce che i suoi autovalori siano
costanti nel tempo; e anche che siano determinabili
con esattezza e simultaneamente agli autovalori di
. Questo garantisce che i suoi autovalori siano
costanti nel tempo; e anche che siano determinabili
con esattezza e simultaneamente agli autovalori di 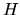 .
.
- Un solo operatore addizionale potrebbe non bastare a
classificare gli stati. Cercherò allora un altro operatore
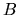 , che deve soddisfare anch'esso a
, che deve soddisfare anch'esso a ![$[B,H]=0$](img374.gif) .
Ma non basta! Occorre anche che sia
.
Ma non basta! Occorre anche che sia ![$[A,B]=0$](img358.gif) . Se così non
fosse, non potrei determinare simultaneamente gli autovalori
di
. Se così non
fosse, non potrei determinare simultaneamente gli autovalori
di 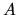 e di
e di 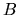 , e quindi un tale schema sarebbe inutile ai
fini della classificazione.
, e quindi un tale schema sarebbe inutile ai
fini della classificazione.
- Ripeto il procedimento finchè sono riuscito a classificare
tutti gli stati, e non esistono altri operatori che commutino
con
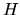 e tutti gli altri.
e tutti gli altri.
- Ho allora costruito un insieme di osservabili che determina
univocamente lo stato del sistema.
Nel caso dell'atomo di idrogeno, come si vedrà, si utilizzano
quattro operatori: 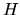 ,
, 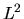 ,
, 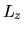 e
e 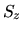 , discussi in seguito.
, discussi in seguito.




Next: Il momento angolare in
Up: Aspetti importanti della meccanica
Previous: Regole di commutazione
Contents
furio
2002-02-24
![]() , e definito
l'operatore
, e definito
l'operatore ![]() in modo tale che per ogni stato dipendente
dal tempo
in modo tale che per ogni stato dipendente
dal tempo ![]() si abbia
si abbia
![]() su uno stato
su uno stato ![]() espanso in termini
di autofunzioni dell'energia, e deriviamola rispetto al tempo,
ottenendo così
espanso in termini
di autofunzioni dell'energia, e deriviamola rispetto al tempo,
ottenendo così
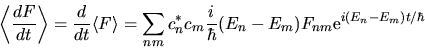
![]() :
:
![]() ,
, ![]() ,
, ![]() e
e ![]() , discussi in seguito.
, discussi in seguito.