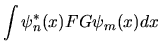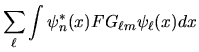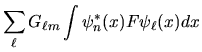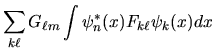Next: Regole di commutazione
Up: Aspetti importanti della meccanica
Previous: Rappresentazioni
Contents
Abbiamo visto che ogni soluzione dell'equazione di Schrödinger
può essere espressa nella forma (3.31).
Note le autofunzioni dell'hamiltoniano, una funzione
d'onda è pertanto caratterizzata dai coefficienti (complessi)
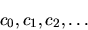 |
(3.42) |
Possiamo pensare a questi numeri come alle componenti di un
vettore in uno spazio dove ogni asse rappresenta una
autofunzione dell'energia.
Poichè la 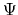 deve essere normalizzata, occorre che sia
deve essere normalizzata, occorre che sia
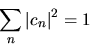 |
(3.43) |
Qual è l'energia media di 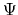 ?
Utilizzando la (3.35) per l'operatore
?
Utilizzando la (3.35) per l'operatore 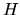 ,
tenendo conto di (3.19) e (3.17),
si trova
,
tenendo conto di (3.19) e (3.17),
si trova
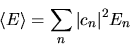 |
(3.44) |
Questo va interpretato nel senso che una misura dell'energia
della funzione darà sempre come risultato uno degli autovalori
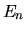 , e a ciascuno di essi è associata una probabilità
, e a ciascuno di essi è associata una probabilità
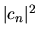 .
.
Supponiamo ora invece di voler calcolare il valor medio
associato ad un generico operatore 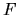 :
:
dove si è definito
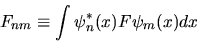 |
(3.48) |
Questa quantità è detta elemento di matrice
dell'operatore 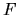 fra gli autostati
fra gli autostati 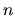 e
e 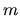 .
Così, in questa formulazione (sviluppata da Heisenberg
prima della scoperta della meccanica ondulatoria) gli stati
sono rappresentati da vettori, e gli operatori da matrici.
In un'altra notazione--sviluppata da Dirac--questo elemento
di matrice è indicato con
.
Così, in questa formulazione (sviluppata da Heisenberg
prima della scoperta della meccanica ondulatoria) gli stati
sono rappresentati da vettori, e gli operatori da matrici.
In un'altra notazione--sviluppata da Dirac--questo elemento
di matrice è indicato con
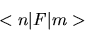 |
(3.49) |
mentre 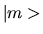 rappresenta un autostato dell'hamiltoniano.
rappresenta un autostato dell'hamiltoniano.
La (3.47) ci dice che un valor medio, in generale,
dipende dal tempo. Vediamo anche che se 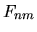 fosse una
matrice diagonale il valor medio sarebbe una costante, in
quanto non vi sarebbe più alcun fattore di fase oscillante
con coefficiente non nullo.
fosse una
matrice diagonale il valor medio sarebbe una costante, in
quanto non vi sarebbe più alcun fattore di fase oscillante
con coefficiente non nullo.
I fattori di fase oscillanti con frequenza
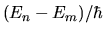 danno dei termini che sono legati a transizioni del sistema
da uno stato ad un altro. Termini di questo tipo si trovano
ad esempio quando si studiano i processi di emissione o
assorbimento di radiazione elettromagnetica (fotoni)
È da notare che--grazie alla doppia sommatoria su
danno dei termini che sono legati a transizioni del sistema
da uno stato ad un altro. Termini di questo tipo si trovano
ad esempio quando si studiano i processi di emissione o
assorbimento di radiazione elettromagnetica (fotoni)
È da notare che--grazie alla doppia sommatoria su 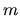 e su
e su 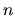 --tutti i termini sono in realtà reali in quanto
per ogni termine viene sommato anche il suo complesso coniugato,
corrispondente allo scambio di indici.
Questo consente di continuare a interpretare i coefficienti
che moltiplicano gli
--tutti i termini sono in realtà reali in quanto
per ogni termine viene sommato anche il suo complesso coniugato,
corrispondente allo scambio di indici.
Questo consente di continuare a interpretare i coefficienti
che moltiplicano gli 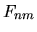 come delle probabilità.
come delle probabilità.
Un operatore 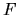 può essere applicato ad una funzione.
In questa rappresentazione matriciale, questa operazione corrisponde ad
applicare una matrice a un vettore, ottenendo un altro vettore. Infatti,
se
può essere applicato ad una funzione.
In questa rappresentazione matriciale, questa operazione corrisponde ad
applicare una matrice a un vettore, ottenendo un altro vettore. Infatti,
se
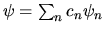 (e ricordando la regola (3.32)
per ottenere le ``componenti del vettore''):
(e ricordando la regola (3.32)
per ottenere le ``componenti del vettore''):
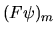 |
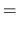 |
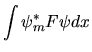 |
(3.50) |
| |
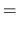 |
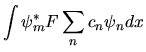 |
(3.51) |
| |
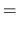 |
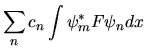 |
(3.52) |
| |
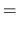 |
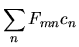 |
(3.53) |
che è la consueta regola dell'algebra lineare.
Notiamo anche che si può espandere
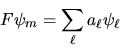 |
(3.54) |
dove i coefficienti sono ottenuti con la consueta regola:
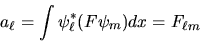 |
(3.55) |
e quindi
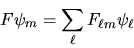 |
(3.56) |
Possiamo infine applicare due operatori 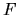 e
e 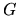 in sequenza, e mostrare come nella rappresentazione
matriciale questa operazione corrisponda ad effettuare un
prodotto tra le due matrici corrispondenti secondo le
consuete regole dell'algebra lineare. Infatti,
usando la (3.56) due volte:
in sequenza, e mostrare come nella rappresentazione
matriciale questa operazione corrisponda ad effettuare un
prodotto tra le due matrici corrispondenti secondo le
consuete regole dell'algebra lineare. Infatti,
usando la (3.56) due volte:
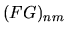 |
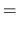 |
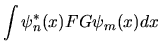 |
(3.57) |
| |
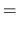 |
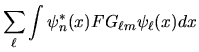 |
(3.58) |
| |
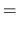 |
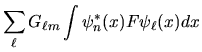 |
(3.59) |
| |
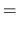 |
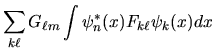 |
(3.60) |
| |
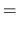 |
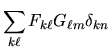 |
(3.61) |
| |
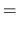 |
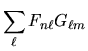 |
(3.62) |
che è appunto l'ordinaria regola per il prodotto di matrici.




Next: Regole di commutazione
Up: Aspetti importanti della meccanica
Previous: Rappresentazioni
Contents
furio
2002-02-24
![]() deve essere normalizzata, occorre che sia
deve essere normalizzata, occorre che sia
![]() :
:
![]() fosse una
matrice diagonale il valor medio sarebbe una costante, in
quanto non vi sarebbe più alcun fattore di fase oscillante
con coefficiente non nullo.
fosse una
matrice diagonale il valor medio sarebbe una costante, in
quanto non vi sarebbe più alcun fattore di fase oscillante
con coefficiente non nullo.
![]() danno dei termini che sono legati a transizioni del sistema
da uno stato ad un altro. Termini di questo tipo si trovano
ad esempio quando si studiano i processi di emissione o
assorbimento di radiazione elettromagnetica (fotoni)
È da notare che--grazie alla doppia sommatoria su
danno dei termini che sono legati a transizioni del sistema
da uno stato ad un altro. Termini di questo tipo si trovano
ad esempio quando si studiano i processi di emissione o
assorbimento di radiazione elettromagnetica (fotoni)
È da notare che--grazie alla doppia sommatoria su ![]() e su
e su ![]() --tutti i termini sono in realtà reali in quanto
per ogni termine viene sommato anche il suo complesso coniugato,
corrispondente allo scambio di indici.
Questo consente di continuare a interpretare i coefficienti
che moltiplicano gli
--tutti i termini sono in realtà reali in quanto
per ogni termine viene sommato anche il suo complesso coniugato,
corrispondente allo scambio di indici.
Questo consente di continuare a interpretare i coefficienti
che moltiplicano gli ![]() come delle probabilità.
come delle probabilità.
![]() può essere applicato ad una funzione.
In questa rappresentazione matriciale, questa operazione corrisponde ad
applicare una matrice a un vettore, ottenendo un altro vettore. Infatti,
se
può essere applicato ad una funzione.
In questa rappresentazione matriciale, questa operazione corrisponde ad
applicare una matrice a un vettore, ottenendo un altro vettore. Infatti,
se
![]() (e ricordando la regola (3.32)
per ottenere le ``componenti del vettore''):
(e ricordando la regola (3.32)
per ottenere le ``componenti del vettore''):
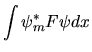
![]() e
e ![]() in sequenza, e mostrare come nella rappresentazione
matriciale questa operazione corrisponda ad effettuare un
prodotto tra le due matrici corrispondenti secondo le
consuete regole dell'algebra lineare. Infatti,
usando la (3.56) due volte:
in sequenza, e mostrare come nella rappresentazione
matriciale questa operazione corrisponda ad effettuare un
prodotto tra le due matrici corrispondenti secondo le
consuete regole dell'algebra lineare. Infatti,
usando la (3.56) due volte: