



Next: La funzione d'onda radiale
Up: Atomi con un elettrone
Previous: Funzioni d'onda angolari
Contents
Il caso più semplice è quello in cui 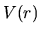 è semplicemente
il potenziale coulombiano:
è semplicemente
il potenziale coulombiano:
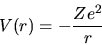 |
(4.25) |
dove 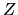 è il numero atomico (numero di protoni nel nucleo)
ed
è il numero atomico (numero di protoni nel nucleo)
ed 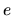 la carica dell'elettrone (
la carica dell'elettrone (
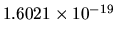 coul).
L'espressione sopra è valida nel sistema CGS; nel sistema MKS
si scrive invece
coul).
L'espressione sopra è valida nel sistema CGS; nel sistema MKS
si scrive invece
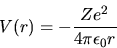 |
(4.26) |
È comodo lavorare in unità atomiche, definite nel
sistema CGS da
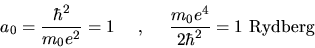 |
(4.27) |
dove 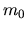 è la massa dell'elettrone (non la massa ridotta,
che dipende dal nucleo considerato).
Nel sistema MKS valgono le stesse definizioni con
è la massa dell'elettrone (non la massa ridotta,
che dipende dal nucleo considerato).
Nel sistema MKS valgono le stesse definizioni con
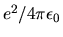 al posto di
al posto di 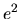 .
.
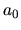 è uguale a
è uguale a
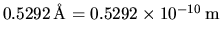 ,
mentre l'unità di energia è detta Rydberg e vale 13.605 eV.
Si usa assai spesso anche l'Hartree:
,
mentre l'unità di energia è detta Rydberg e vale 13.605 eV.
Si usa assai spesso anche l'Hartree:
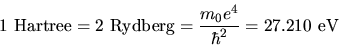 |
(4.28) |
In unità atomiche anche 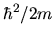 vale 1, e l'equazione di
Schrödinger radiale si scrive
[si immagini di moltiplicare la (4.17) per
vale 1, e l'equazione di
Schrödinger radiale si scrive
[si immagini di moltiplicare la (4.17) per
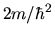 ]
]
![\begin{displaymath}
-\frac{1}{r^2}
\frac{\partial}{\partial r}
\left( r^2 \frac{...
...ll(\ell+1)}{r^2} \right] R_{n\ell}(r)
= E_{n\ell} R_{n\ell}(r)
\end{displaymath}](img583.gif) |
(4.29) |
che possiamo in realtà ritenere anche una espressione
valida per il caso di un potenziale generico, qualora si
consideri 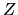 essere una funzione di
essere una funzione di 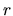 anzichè una costante.
anzichè una costante.




Next: La funzione d'onda radiale
Up: Atomi con un elettrone
Previous: Funzioni d'onda angolari
Contents
furio
2002-02-24
![]() è semplicemente
il potenziale coulombiano:
è semplicemente
il potenziale coulombiano:
![]() vale 1, e l'equazione di
Schrödinger radiale si scrive
[si immagini di moltiplicare la (4.17) per
vale 1, e l'equazione di
Schrödinger radiale si scrive
[si immagini di moltiplicare la (4.17) per
![]() ]
]