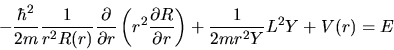Next: Funzioni d'onda angolari
Up: Atomi con un elettrone
Previous: Equazione di Schrödinger in
Contents
Separazione in parte radiale e angolare
Introduciamo, analogamente a quanto fatto nella sezione
3.9, un sistema di riferimento polare
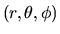 , dove l'operatore gradiente è
dato dalla (3.95), e l'operatore laplaciano
(come si può far vedere con un po' di pazienza) da
, dove l'operatore gradiente è
dato dalla (3.95), e l'operatore laplaciano
(come si può far vedere con un po' di pazienza) da
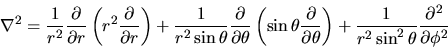 |
(4.8) |
Confrontando con la (3.101), si vede che questo si
può scrivere
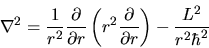 |
(4.9) |
dove 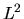 dato dalla (3.101) contiene esclusivamente
termini dipendenti dagli angoli.
Possiamo allora scrivere l'hamiltoniano come
dato dalla (3.101) contiene esclusivamente
termini dipendenti dagli angoli.
Possiamo allora scrivere l'hamiltoniano come
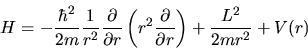 |
(4.10) |
Un termine 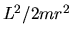 appare anche nell'analogo problema classico:
altri non è che il ``potenziale centrifugo'', ossia un potenziale
fittizio che genera una ``forza'' che tende ad allontanare la
massa dall'origine, e che discende dal fatto che il sistema
è in rotazione (se
appare anche nell'analogo problema classico:
altri non è che il ``potenziale centrifugo'', ossia un potenziale
fittizio che genera una ``forza'' che tende ad allontanare la
massa dall'origine, e che discende dal fatto che il sistema
è in rotazione (se 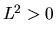 ), e che noi stiamo osservando la
sola variabile radiale.
Classicamente si può dunque tener conto dell'effetto della rotazione
considerando un potenziale efficace
), e che noi stiamo osservando la
sola variabile radiale.
Classicamente si può dunque tener conto dell'effetto della rotazione
considerando un potenziale efficace
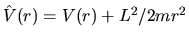 , dove il secondo termine tende a
spingere la massa verso gli
, dove il secondo termine tende a
spingere la massa verso gli 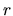 crescenti.
crescenti.
Vediamo ora la situazione nel caso quantistico.
Un'ispezione della forma (4.10) ci mostra subito che
![\begin{displaymath}[L^2,H]= 0
\end{displaymath}](img534.gif) |
(4.11) |
che ci garantisce che 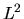 è conservato, ossia i suoi
autovalori non dipendono dal tempo e i due operatori hanno
un insieme di autostati in comune. Già sappiamo quindi
che gli autovalori di
è conservato, ossia i suoi
autovalori non dipendono dal tempo e i due operatori hanno
un insieme di autostati in comune. Già sappiamo quindi
che gli autovalori di 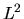 potranno essere usati per classificare
gli stati.
L'espressione (3.100) per
potranno essere usati per classificare
gli stati.
L'espressione (3.100) per 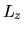 e la regola
(3.93) ci dicono anche che
e la regola
(3.93) ci dicono anche che
![\begin{displaymath}[L_z,H]= 0
\end{displaymath}](img535.gif) |
(4.12) |
e quindi anche gli autovalori di 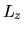 saranno conservati e
potranno essere usati per classificare gli stati.
saranno conservati e
potranno essere usati per classificare gli stati.
Procediamo ora alla separazione della variabile radiale da quelle
angolari, la cui possibilità fortemente suggerita sia
da questi risultati che dall'osservazione della (4.10).
Poniamo
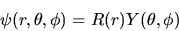 |
(4.13) |
quindi riscriviamo l'equazione di Schrödinger (4.7),
dividendola per 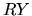 :
:
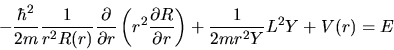 |
(4.14) |
o ancora moltiplicando per
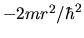 e riarrangiando,
e riarrangiando,
![\begin{displaymath}
\frac{1}{R(r)} \frac{\partial}{\partial r}
\left( r^2 \frac{...
...{\hbar^2} \left[ V(r) - E \right] =
\frac{1}{\hbar^2 Y} L^2 Y
\end{displaymath}](img540.gif) |
(4.15) |
Il membro sinistro dipende solo da 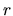 , quello destro solo da
, quello destro solo da
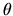 e
e 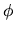 , e quindi entrambi devono essere uguali ad una
costante. Abbiamo già [vedi (3.102)] indicato questa
costante con
, e quindi entrambi devono essere uguali ad una
costante. Abbiamo già [vedi (3.102)] indicato questa
costante con 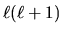 , e trovato che
, e trovato che 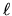 deve essere
un intero affinchè la soluzione non diverga.
Le soluzioni per la parte angolare sono le armoniche sferiche
deve essere
un intero affinchè la soluzione non diverga.
Le soluzioni per la parte angolare sono le armoniche sferiche
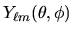 date dalla (3.110).
Dovrà quindi essere
date dalla (3.110).
Dovrà quindi essere
![\begin{displaymath}
\frac{1}{R(r)} \frac{\partial}{\partial r}
\left( r^2 \frac...
...- \frac{2mr^2}{\hbar^2} \left[ V(r) - E \right] =
\ell(\ell+1)
\end{displaymath}](img543.gif) |
(4.16) |
ovvero l'equazione di Schrödinger per la parte radiale è
![\begin{displaymath}
-\frac{\hbar^2}{2m} \frac{1}{r^2}
\frac{\partial}{\partial r...
...(\ell+1)}{2mr^2} \right] R_{n\ell}(r)
= E_{n\ell} R_{n\ell}(r)
\end{displaymath}](img544.gif) |
(4.17) |
Ci aspettiamo che in generale le energie dipendano da 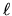 perchè il potenziale efficace dipende da
perchè il potenziale efficace dipende da 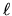 ; inoltre
per un dato
; inoltre
per un dato 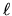 ci aspettiamo per gli stati legati
(se ve ne sono!) una quantizzazione dei livelli energetici,
e abbiamo indicato con
ci aspettiamo per gli stati legati
(se ve ne sono!) una quantizzazione dei livelli energetici,
e abbiamo indicato con 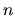 il corrispondente indice.
il corrispondente indice.
La funzione d'onda totale sarà allora
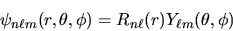 |
(4.18) |
L'energia non dipende da 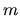 . Come già osservato,
. Come già osservato, 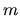 rappresenta la proiezione del momento angolare su un asse
scelto arbitrariamente. A causa della simmetria sferica del
problema, l'energia non può dipendere dall'orientamento
del vettore
rappresenta la proiezione del momento angolare su un asse
scelto arbitrariamente. A causa della simmetria sferica del
problema, l'energia non può dipendere dall'orientamento
del vettore 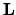 , ma solo dal suo modulo.
All'energia
, ma solo dal suo modulo.
All'energia 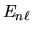 sarà dunque associata una degenerazione
sarà dunque associata una degenerazione
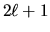 (o maggiore, se esistono altri osservabili commutanti
che non abbiamo considerato!).
(o maggiore, se esistono altri osservabili commutanti
che non abbiamo considerato!).
Subsections




Next: Funzioni d'onda angolari
Up: Atomi con un elettrone
Previous: Equazione di Schrödinger in
Contents
furio
2002-02-24
![]() , dove l'operatore gradiente è
dato dalla (3.95), e l'operatore laplaciano
(come si può far vedere con un po' di pazienza) da
, dove l'operatore gradiente è
dato dalla (3.95), e l'operatore laplaciano
(come si può far vedere con un po' di pazienza) da
![]() appare anche nell'analogo problema classico:
altri non è che il ``potenziale centrifugo'', ossia un potenziale
fittizio che genera una ``forza'' che tende ad allontanare la
massa dall'origine, e che discende dal fatto che il sistema
è in rotazione (se
appare anche nell'analogo problema classico:
altri non è che il ``potenziale centrifugo'', ossia un potenziale
fittizio che genera una ``forza'' che tende ad allontanare la
massa dall'origine, e che discende dal fatto che il sistema
è in rotazione (se ![]() ), e che noi stiamo osservando la
sola variabile radiale.
Classicamente si può dunque tener conto dell'effetto della rotazione
considerando un potenziale efficace
), e che noi stiamo osservando la
sola variabile radiale.
Classicamente si può dunque tener conto dell'effetto della rotazione
considerando un potenziale efficace
![]() , dove il secondo termine tende a
spingere la massa verso gli
, dove il secondo termine tende a
spingere la massa verso gli ![]() crescenti.
crescenti.