



Next: Il metodo variazionale in
Up: Metodo variazionale
Previous: Dimostrazione del principio variazionale
Contents
Siano 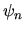 gli autostati di un hamiltoniano
gli autostati di un hamiltoniano 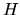 ,
a cui sono associate energie
,
a cui sono associate energie 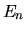 :
:
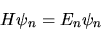 |
(5.46) |
Supponiamo che lo stato fondamentale corrisponda a 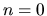 e abbia quindi energia
e abbia quindi energia 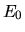 .
Sia
.
Sia 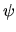 una qualunque altra funzione. Dimostriamo che si ha
necessariamente
una qualunque altra funzione. Dimostriamo che si ha
necessariamente
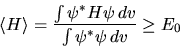 |
(5.47) |
Per dimostrarlo, pensiamo di sviluppare 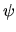 usando la base
delle autofunzioni dell'energia. Ciò è sempre possibile
perchè le autofunzioni dell'energia costituiscono un sistema
completo e ortonormale, come dimostrato in 3.2.
usando la base
delle autofunzioni dell'energia. Ciò è sempre possibile
perchè le autofunzioni dell'energia costituiscono un sistema
completo e ortonormale, come dimostrato in 3.2.
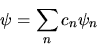 |
(5.48) |
Sarà allora
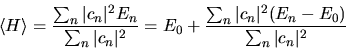 |
(5.49) |
Poichè il secondo termine è positivo o nullo, essendo
per definizione di stato fondamentale 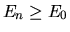 , la
(5.47) è dimostrata.
, la
(5.47) è dimostrata.
Questo risultato è semplice ma estremamente importante: ci dice
che data una qualsiasi 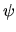 , il suo valor medio dell'energia
è sempre una stima superiore dell'energia dello stato fondamentale.
Se lo stato fondamentale non è noto, si può quindi pensare di
cercare una sua approssimazione facendo variare
, il suo valor medio dell'energia
è sempre una stima superiore dell'energia dello stato fondamentale.
Se lo stato fondamentale non è noto, si può quindi pensare di
cercare una sua approssimazione facendo variare 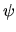 nell'ambito
di un insieme di funzioni di prova e cercando quella funzione che
minimizza
nell'ambito
di un insieme di funzioni di prova e cercando quella funzione che
minimizza
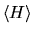 . Questa è l'essenza del
metodo variazionale.
. Questa è l'essenza del
metodo variazionale.




Next: Il metodo variazionale in
Up: Metodo variazionale
Previous: Dimostrazione del principio variazionale
Contents
furio
2002-02-24
![]() gli autostati di un hamiltoniano
gli autostati di un hamiltoniano ![]() ,
a cui sono associate energie
,
a cui sono associate energie ![]() :
:
![]() , il suo valor medio dell'energia
è sempre una stima superiore dell'energia dello stato fondamentale.
Se lo stato fondamentale non è noto, si può quindi pensare di
cercare una sua approssimazione facendo variare
, il suo valor medio dell'energia
è sempre una stima superiore dell'energia dello stato fondamentale.
Se lo stato fondamentale non è noto, si può quindi pensare di
cercare una sua approssimazione facendo variare ![]() nell'ambito
di un insieme di funzioni di prova e cercando quella funzione che
minimizza
nell'ambito
di un insieme di funzioni di prova e cercando quella funzione che
minimizza
![]() . Questa è l'essenza del
metodo variazionale.
. Questa è l'essenza del
metodo variazionale.