



Next: Esempio: trattamento variazionale dell'atomo
Up: Metodo variazionale
Previous: Energia dello stato fondamentale
Contents
Si identifica una famiglia di funzioni d'onda di prova
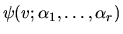 , dove
, dove 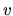 è l'insieme delle
variabili, e gli
è l'insieme delle
variabili, e gli 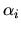 sono parametri.
L'autovalore dell'energia sarà una funzione del parametri:
sono parametri.
L'autovalore dell'energia sarà una funzione del parametri:
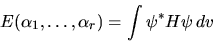 |
(5.50) |
Il metodo variazionale consiste nel cercare il minimo di
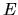 rispetto a variazioni dei parametri, imponendo cioè
rispetto a variazioni dei parametri, imponendo cioè
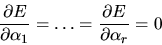 |
(5.51) |
La 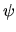 che soddisfa a queste condizioni con l'energia
più bassa è quella che più si avvicina allo
stato fondamentale.
Può essere considerata come la miglior approssimazione
possibile allo stato fondamentale tra l'insieme delle
funzioni di prova.
che soddisfa a queste condizioni con l'energia
più bassa è quella che più si avvicina allo
stato fondamentale.
Può essere considerata come la miglior approssimazione
possibile allo stato fondamentale tra l'insieme delle
funzioni di prova.
È chiaro che la scelta della famiglia delle funzioni di
prova gioca un ruolo cruciale e va effettuata con attenzione.
furio
2002-02-24
![]() , dove
, dove ![]() è l'insieme delle
variabili, e gli
è l'insieme delle
variabili, e gli ![]() sono parametri.
L'autovalore dell'energia sarà una funzione del parametri:
sono parametri.
L'autovalore dell'energia sarà una funzione del parametri: