



Next: Problema secolare
Up: Metodo variazionale
Previous: Il metodo variazionale in
Contents
Esempio: trattamento variazionale dell'atomo di elio
Un esempio di applicazione del metodo variazionale può
essere fornito nuovamente dall'atomo di elio.
L'hamitoniano, già incontrato in 5.1.1, è
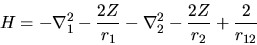 |
(5.52) |
con 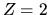 .
Se non vi fosse il termine di repulsione fra i due elettroni
il problema sarebbe separabile. Per ciascun elettrone si
avrebbe uno stato fondamentale
.
Se non vi fosse il termine di repulsione fra i due elettroni
il problema sarebbe separabile. Per ciascun elettrone si
avrebbe uno stato fondamentale
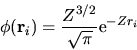 |
(5.53) |
con energia associata 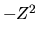 ,
e il loro prodotto sarebbe lo stato fondamentale del
sistema a due elettroni
,
e il loro prodotto sarebbe lo stato fondamentale del
sistema a due elettroni
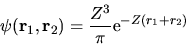 |
(5.54) |
con energia associata 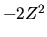 , ossia
, ossia 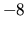 .
Questo scenario implica l'aver assegnato spin opposti ai due
elettroni, averli quindi collocati entrambi in uno stato 1s
(
.
Questo scenario implica l'aver assegnato spin opposti ai due
elettroni, averli quindi collocati entrambi in uno stato 1s
(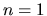 ,
, 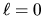 ), e aver costruito una funziona d'onda
complessiva antisimmetrica in cui la parte di spin è
antisimmetrica e quella orbitale simmetrica.
), e aver costruito una funziona d'onda
complessiva antisimmetrica in cui la parte di spin è
antisimmetrica e quella orbitale simmetrica.
L'effetto di ciascun elettrone sull'altro
sarà quello di schermare parzialmente il nucleo.
Per tener conto della repulsione fra elettroni,
possiamo pensare di adottare delle funzioni
di prova del tipo (5.54), in cui però sostituiamo
la vera carica del nucleo 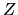 con una ``carica efficace''
con una ``carica efficace'' 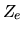 ,
che ci aspettiamo essere più piccola di
,
che ci aspettiamo essere più piccola di 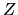 .
Questo sarà il parametro che cercheremo di ottimizzare in
modo variazionale. Assumiamo dunque
.
Questo sarà il parametro che cercheremo di ottimizzare in
modo variazionale. Assumiamo dunque
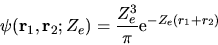 |
(5.55) |
e riscriviamo così l'hamiltoniano:
![\begin{displaymath}
H = \left[
- \nabla_1^2 -\frac{2Z_e}{r_1}
- \nabla_2^2 -\fra...
...Z-Z_e)}{r_1}
-\frac{2(Z-Z_e)}{r_2}
+ \frac{2}{r_{12}}
\right]
\end{displaymath}](img759.gif) |
(5.56) |
Calcoliamo ora
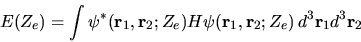 |
(5.57) |
Il contributo all'energia dovuto alla prima parentesi quadra in
(5.56) è 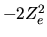 : si tratta infatti di un
problema idrogenoide con nucleo di carica
: si tratta infatti di un
problema idrogenoide con nucleo di carica 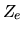 e due
elettroni non interagenti.
Sviluppando gli integrali rimanenti (e notando che due di essi
sono uguali per simmetria) sarà quindi
e due
elettroni non interagenti.
Sviluppando gli integrali rimanenti (e notando che due di essi
sono uguali per simmetria) sarà quindi
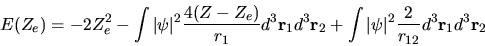 |
(5.58) |
con
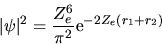 |
(5.59) |
Gli integrali possono essere calcolati e il risultato è
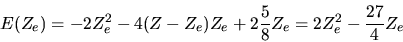 |
(5.60) |
(dove si è esplicitamente inserito 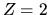 ).
).
La minimizzazione di 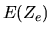 rispetto a
rispetto a 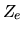 porta immediatamente a
porta immediatamente a
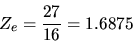 |
(5.61) |
e corrispondentemente
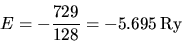 |
(5.62) |
Il risultato è decisamente migliore di quello (
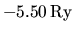 ) ottenuto
col metodo perturbativo, anche se esiste ancora una discrepanza
non trascurabile rispetto al valore sperimentale (
) ottenuto
col metodo perturbativo, anche se esiste ancora una discrepanza
non trascurabile rispetto al valore sperimentale (
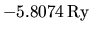 ).
).
Naturalmente è possibile migliorare il risultato variazionale
adottando funzioni di prova più ricche. Questo è quanto
viene effettuato dal metodo di Hartree-Fock descritto nel
prossimo capitolo, in cui la funzione
d'onda complessiva è ancora scritta come un prodotto di
funzioni a un elettrone, le quali vengono però ottimizzate
(ossia non sono semplici esponenziali).
Risultati ancora migliori possono essere ottenuti mediante
funzioni di prova più complesse di un semplice prodotto.




Next: Problema secolare
Up: Metodo variazionale
Previous: Il metodo variazionale in
Contents
furio
2002-02-24
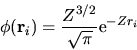
![]() con una ``carica efficace''
con una ``carica efficace'' ![]() ,
che ci aspettiamo essere più piccola di
,
che ci aspettiamo essere più piccola di ![]() .
Questo sarà il parametro che cercheremo di ottimizzare in
modo variazionale. Assumiamo dunque
.
Questo sarà il parametro che cercheremo di ottimizzare in
modo variazionale. Assumiamo dunque
![]() rispetto a
rispetto a ![]() porta immediatamente a
porta immediatamente a