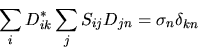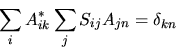Next: Programma: hydrogen_gauss
Up: Problema secolare
Previous: Sviluppo in funzioni ortonormali
Contents
I metodi di algebra di lineare permettono di trattare agevolmente
anche il caso in cui la base è costituita da funzioni
non ortonormali tra loro, in cui cioè
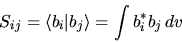 |
(5.79) |
non è pari a 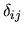 . Gli
. Gli 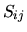 vengono detti
integrali di overlap, per ovvi motivi.
Talvolta risulta comodo lavorare con basi di questo tipo.
vengono detti
integrali di overlap, per ovvi motivi.
Talvolta risulta comodo lavorare con basi di questo tipo.
Considerazioni simili a quelle effettuate all'inizio della
sezione precedente indicano che in questo caso la
(5.66) assume la forma più generale
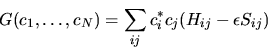 |
(5.80) |
e la condizione di minimo (5.70) diventa
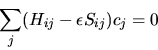 |
(5.81) |
o in forma matriciale
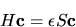 |
(5.82) |
noto come problema agli autovalori generalizzato.
Risolvere un problema agli autovalori generalizzato
corrisponde dal punto di vista numerico a risolvere due problemi
agli autovalori semplici.
Supponiamo infatti di procedere in due stadi, occupandosi
prima del problema ausiliario
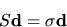 |
(5.83) |
Questo è del tutto analogo al problema (5.72).
Potremo così trovare una matrice 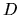 (ottenuta disponendo
gli autovettori per colonne), tale che
(ottenuta disponendo
gli autovettori per colonne), tale che 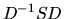 sia
diagonale, e i cui elementi non nulli siano gli autovalori
sia
diagonale, e i cui elementi non nulli siano gli autovalori 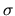 .
Si otterrà una equazione analoga alla (5.78):
.
Si otterrà una equazione analoga alla (5.78):
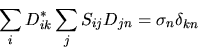 |
(5.84) |
Supponiamo però di definire un'altra matrice di trasformazione
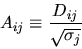 |
(5.85) |
Si avrà allora
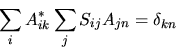 |
(5.86) |
o in forma matriciale
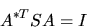 |
(5.87) |
dove 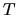 indica trasposizione.
Una matrice
indica trasposizione.
Una matrice 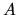 con questa proprietà
può dunque essere ottenuta risolvendo
un normale problema agli autovalori.
con questa proprietà
può dunque essere ottenuta risolvendo
un normale problema agli autovalori.
Poniamo ora
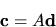 |
(5.88) |
Con questa posizione, l'equazione (5.82) diventa
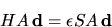 |
(5.89) |
Moltiplichiamo a sinistra per 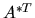 :
:
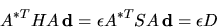 |
(5.90) |
Pertanto, se risolviamo ora il problema secolare per l'operatore
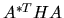 troveremo gli autovalori desiderati per l'energia.
Per ottenere gli autovettori nella nostra base di partenza
basterà, secondo la (5.88), applicare l'operatore
troveremo gli autovalori desiderati per l'energia.
Per ottenere gli autovettori nella nostra base di partenza
basterà, secondo la (5.88), applicare l'operatore 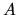 su ciascun autovettore.
su ciascun autovettore.




Next: Programma: hydrogen_gauss
Up: Problema secolare
Previous: Sviluppo in funzioni ortonormali
Contents
furio
2002-02-24