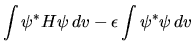 |
(5.63) |
Il metodo variazionale può essere ricondotto ad un problema
algebrico immaginando di sviluppare la funzione d'onda
in una base finita di funzioni, e applicando il metodo
variazionale per trovare i coefficienti ottimali dello sviluppo.
Basandoci sulla (5.38), ciò significa
calcolare il funzionale (ossia una funzione di
funzione)
È fondamentale notare che la nostra base è costituita da
un numero finito ![]() di funzioni, e quindi non costituirà
un sistema completo: ossia non sarà in generale
possibile espandere una qualsiasi funzione
di funzioni, e quindi non costituirà
un sistema completo: ossia non sarà in generale
possibile espandere una qualsiasi funzione ![]() in questa base, tra cui in generale anche le
soluzioni esatte dell'equazione di Schrödinger.
Quello che faremo è quindi trovare la
in questa base, tra cui in generale anche le
soluzioni esatte dell'equazione di Schrödinger.
Quello che faremo è quindi trovare la ![]() che meglio
si avvicina al vero stato fondamentale nell'ambito di tutte
le funzioni esprimibili come combinazione lineare delle
che meglio
si avvicina al vero stato fondamentale nell'ambito di tutte
le funzioni esprimibili come combinazione lineare delle
![]() funzioni di base scelte.
funzioni di base scelte.