Next: Significato del potenziale di
Up: Il metodo di Hartree
Previous: Il metodo di Hartree
Contents
L'hamiltoniano di un atomo con nucleo di carica 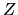 ed
ed 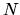 elettroni è (in unità Rydberg)
elettroni è (in unità Rydberg)
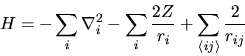 |
(6.21) |
dove le parentesi angolari in
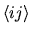 significano
che la somma va limitata a tutte le coppie, ossia implica che
significano
che la somma va limitata a tutte le coppie, ossia implica che
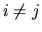 e che ciascuna coppia viene considerata una volta sola.
Ad esempio una scelta valida potrebbe essere
e che ciascuna coppia viene considerata una volta sola.
Ad esempio una scelta valida potrebbe essere
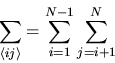 |
(6.22) |
Per futura economia di notazione, e anche per maggiore
generalità delle formule che ricaveremo, definiamo gli operatori
a uno e a due elettroni come
Con questa notazione l'hamiltoniano si scrive
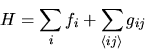 |
(6.25) |
Per usare questa notazione in modo generale è necessario assumere
che 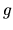 agisca simmetricamente sui due elettroni (cosa
senz'altro vera per l'interazione coulombiana).
agisca simmetricamente sui due elettroni (cosa
senz'altro vera per l'interazione coulombiana).
Supponiamo allora che la funzione d'onda totale sia esprimibile
in forma di prodotto di funzioni d'onda a un elettrone, che
supporremo ortonormali fra loro:
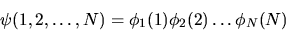 |
(6.26) |
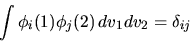 |
(6.27) |
In 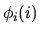 , l'argomento
, l'argomento 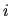 significa: le variabili associate
all'elettrone
significa: le variabili associate
all'elettrone 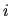 , ossia in pratica la sua posizione e la
proiezione del suo momento angolare di spin.
, ossia in pratica la sua posizione e la
proiezione del suo momento angolare di spin.
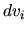 indica un'integrazione rispetto a tutte queste variabili
(e quindi anche una somma sugli spin). Invece l'indice
indica un'integrazione rispetto a tutte queste variabili
(e quindi anche una somma sugli spin). Invece l'indice
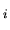 significa: l'insieme dei numeri quantici con cui cataloghiamo
una particolare autofunzione, ossia in pratica (nel caso del
campo centrale, che come vedremo è quello che ci interessa)
il numero quantico principale
significa: l'insieme dei numeri quantici con cui cataloghiamo
una particolare autofunzione, ossia in pratica (nel caso del
campo centrale, che come vedremo è quello che ci interessa)
il numero quantico principale 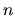 , il momento angolare orbitale
, il momento angolare orbitale
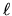 e la sua proiezione
e la sua proiezione 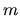 .
.
Procediamo col calcolare il valor medio dell'energia:
Nel primo passaggio si è fatto uso dell'ortonormalità
(6.27); nel secondo si è semplicemente effettuata
una sostituzione delle variabili di integrazione, che non
giocano alcun ruolo, standardizzandole a 1 e 2 per comodità.
Applichiamo ora il principio variazionale nella formulazione
(5.38), richiedendo che nella variazione restino
stazionari anche tutti gli integrali
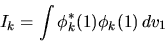 |
(6.29) |
affinchè la normalizzazione di ogni funzione orbitale
venga preservata. Vogliamo quindi imporre
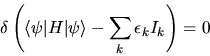 |
(6.30) |
dove gli 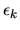 sono i moltiplicatori di Lagrange da determinare.
Supponiamo che venga fatta variare soltanto la funzione orbitale
con indice
sono i moltiplicatori di Lagrange da determinare.
Supponiamo che venga fatta variare soltanto la funzione orbitale
con indice 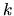 . Si ha allora
. Si ha allora
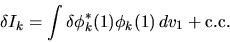 |
(6.31) |
(mentre le variazioni di tutti gli altri integrali di
normalizzazione saranno ovviamente nulle)
ed anche, seguendo le argomentazioni in 5.2.1
sull'hermiticità di 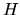 ,
,
Questo si ottiene notando che gli unici termini della
(6.28) interessati sono quelli con
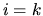 oppure
oppure 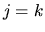 , e che ogni coppia è contata una e una sola volta.
Ad esempio per 4 elettroni le coppie sono 12, 13, 14, 23, 24, 34;
se scelgo
, e che ogni coppia è contata una e una sola volta.
Ad esempio per 4 elettroni le coppie sono 12, 13, 14, 23, 24, 34;
se scelgo 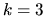 viene un contributo solo da 13, 23 e 34, che
corrisponde a una
viene un contributo solo da 13, 23 e 34, che
corrisponde a una 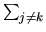 (l'ordine in cui appaiono
gli indici della coppia non ha importanza, essendo
(l'ordine in cui appaiono
gli indici della coppia non ha importanza, essendo 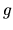 un
operatore simmetrico).
un
operatore simmetrico).
Pertanto, il principio variazionale assume la forma
Affinchè il principio variazionale sia soddisfatto,
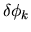 deve essere considerata una variazione arbitraria,
e quindi il termine tra le parentesi quadrate deve essere nullo
(assieme al suo complesso coniugato!).
Deve quindi essere verificata
deve essere considerata una variazione arbitraria,
e quindi il termine tra le parentesi quadrate deve essere nullo
(assieme al suo complesso coniugato!).
Deve quindi essere verificata
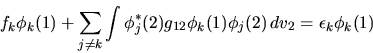 |
(6.33) |
Queste (per 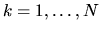 ) sono le equazioni di Hartree.
È utile scriverle mettendo gli operatori in forma esplicita:
) sono le equazioni di Hartree.
È utile scriverle mettendo gli operatori in forma esplicita:
![\begin{displaymath}
-\nabla^2_k \phi_k(1) -\frac{2Z}{r_1} \phi_k(1) +
\left[ \s...
...}}
\phi_j(2) \, dv_2 \right] \phi_k(1) = \epsilon_k \phi_k(1)
\end{displaymath}](img933.gif) |
(6.34) |
Osserviamo che ciascuna di esse è simile ad una equazione
di Schrödinger, in cui al potenziale coulombiano si aggiunge
il ``potenziale di Hartree''
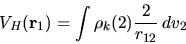 |
(6.35) |
dove si è posto
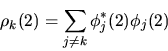 |
(6.36) |
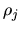 è la densità dovuta a tutti gli elettroni diversi
da quello per cui stiamo scrivendo l'equazione.
La (6.35) rappresenta il potenziale elettrostatico
nel punto
è la densità dovuta a tutti gli elettroni diversi
da quello per cui stiamo scrivendo l'equazione.
La (6.35) rappresenta il potenziale elettrostatico
nel punto 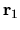 generato da una distribuzione spaziale
di carica
generato da una distribuzione spaziale
di carica 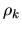 .
Nel metodo di Hartree si adotta una ulteriore approssimazione,
che è quella di assumere che
.
Nel metodo di Hartree si adotta una ulteriore approssimazione,
che è quella di assumere che 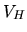 sia un campo centrale,
ossia dipenda dalla sola distanza
sia un campo centrale,
ossia dipenda dalla sola distanza 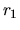 dell'elettrone dal
nucleo. Ciò corrispondere ad effettuare una operazione
di media sferica nella definizione di
dell'elettrone dal
nucleo. Ciò corrispondere ad effettuare una operazione
di media sferica nella definizione di 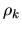 .
.




Next: Significato del potenziale di
Up: Il metodo di Hartree
Previous: Il metodo di Hartree
Contents
furio
2002-02-24
![]() ed
ed ![]() elettroni è (in unità Rydberg)
elettroni è (in unità Rydberg)
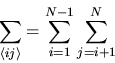
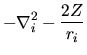
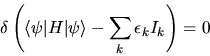
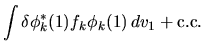
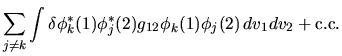
![$\displaystyle \int \delta\phi^*_k(1)
\left[
f_k \phi_k(1)
+ \sum_{j\ne k}
\int ...
...\phi_k(1) \phi_j(2) \, dv_2
- \epsilon_k \phi_k(1) \right] \, dv_1 + {\rm c.c.}$](img929.gif)