The increasing complexity of realistic models and the evolution of the computational platforms and architectures are challenging the numerical analysis community to develop more efficient, effective, and innovative methods, able to incorporate uncertainty quantification, data analysis and high performance computing applications. 

The main goal of the project “Numerical Analysis of Full and Reduced order Methods for Partial Differential Equations” (NA_FROM-PDEs) is to design and analyze innovative numerical methods and methodologies for the approximation of partial differential equations (PDEs) in computational sciences and engineering. 

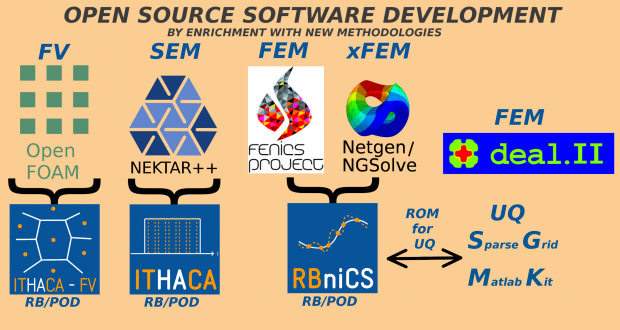
The research units  in SISSA, CNR, Pavia, Milano, Torino, and Trento share a consolidated expertise on advanced discretization schemes based on variational approaches, such as conforming and nonconforming Finite Elements (FEM), spectral and hp Finite Elements (hp-FEM), immersed methods, Finite Volumes (FV), as well as on Reduced Order Methods (ROMs) that rely on the aforementioned schemes and on Uncertainty Quantification (UQ) methodologies.

An important product of our research will be the development of software and the release of new libraries within open source projects. In particular, we plan to continue our support to the maintenance of the open source libraries RBniCS, ITHACA, deal.II and the Sparse Grids Matlab Kit. 

It is expected that these tools will emerge as efficient computational platforms for complex problems, and will be proposed not only to project partners, but also to broader audience (national and international, academic and non-academic). 

The project is founded by MIUR through PRIN 2017.

Keywords: Partial Differential Equations, Reduced Order Model, Full Order Models, Uncertainty Quantification, Finite Element, Finite Volume, Immersed Method, hp-FEM, High Performance Computing, Fluid Structure Interactions.