The increasing complexity of realistic models and the evolution of the computational platforms and architectures are challenging the numerical analysis community to develop more efficient, effective, and innovative methods, able to incorporate uncertainty quantification, data analysis and high performance computing applications.
The research units share a consolidated expertise on advanced discretisation schemes based on variational approaches, such as conforming and nonconforming finite elements, spectral and hp type finite elements, immersed methods, finite volumes (FV) and reduced order methods which rely on these schemes. We focus on full and reduced order methods to study how the possible uncertain/incomplete knowledge of the parameters of the PDEs, due e.g. to intrinsic variability or measurement errors, affects the outcomes of the computations.
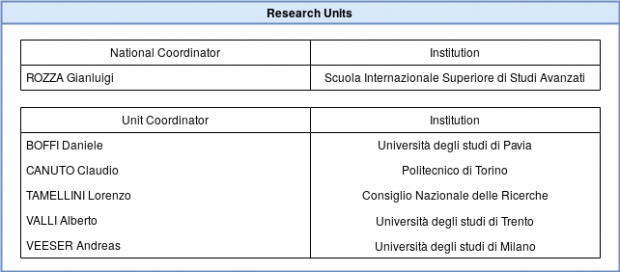
ROZZA Gianluigi, Full Professor at SISSA, grozza@sissa.it
BOFFI Daniele, Full Professor at Universita’ degli studi di Pavia, daniele.boffi@unipv.it
CANUTO Claudio, Full Professor at Politecnico di Torino, claudio.canuto@polito.it
TAMELLINI Lorenzo Resercher at IMATI-CNR, tamellini@imati.cnr.it
VALLI Alberto, Full Professor at Universita’ degli studi di Trento, valli@science.unitn.it
VEESER Andreas, Full Professor at Universita’ degli studi di Milano, andreas.veeser@polimi.it
A new research position in Mathematics area within the group is now available. To learn more: Selezione pubblica per titoli per il conferimento di n. 1 assegno di ricerca – Area Matematica (ref. prof. Rozza) | Scuola Internazionale Superiore di Studi Avanzati (sissa.it)
To apply (with deadline March 24 at 1pm): https://pica.cineca.it/sissa/ar-fe-mate-6-2022