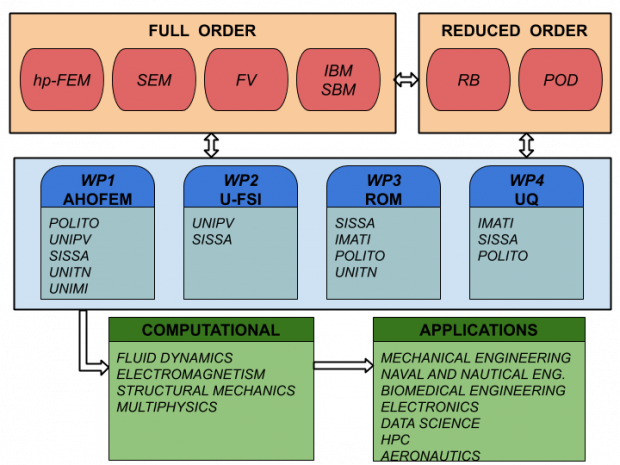
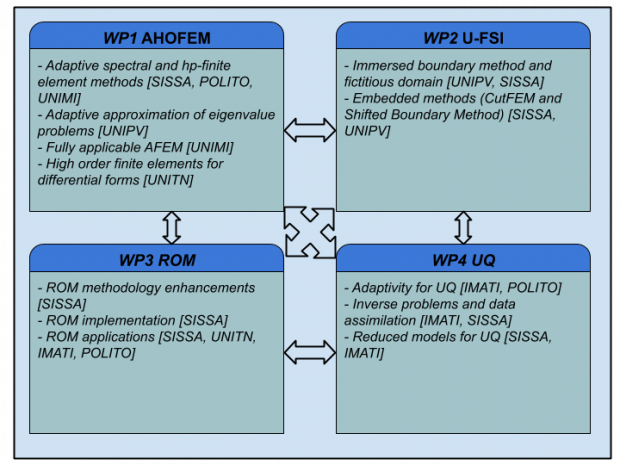
Work Packages
The research units share a consolidated expertise on advanced discretisation schemes based on variational approaches, such as conforming and nonconforming finite elements, spectral and hp type finite elements, immersed methods, finite volumes (FV) and reduced order methods which rely on these schemes. We focus on full and reduced order methods to study how the possible uncertain/incomplete knowledge of the parameters of the PDEs, due e.g. to intrinsic variability or measurement errors, affects the outcomes of the computations.
The final goal is the creation of a suit of numerical tools (based on both Full Order and Reduced Order Models) for the efficient solution of problems involving fluid dynamics, electromagnetism, structural mechanics, and multiphysics.
The developed software will be useful in many different fields, with applications in automotive, aeronautics, biomedical engineering, HPC, data science, and nautical engineering.
The project is organised in four work packages (WP):
WP1: Adaptive and High Order Finite Element Methods
WP2: Unfitted methods for Fluid-Structure Interactions
WP3: Reduced Order Methods
WP4: Uncertainty Quantification, model reduction, and data.
WP1. AHOFEM: Adaptive and High Order Finite Element Methods
[POLITO, UNIMI, UNIPV, SISSA, UNITN]
The accurate approximation of multiphysics problems with possible singular solutions requires the use of suitably adapted computational meshes and/or high order methods.
We plan to study the convergence properties and the optimal complexity of adaptive processes for advanced and non-standard discretisations, including the approximation of eigenvalue problems. New challenges consist in coupling h- and p-adaptivity for hp-FEM schemes and in dealing with any data that is admissible for the weak formulation of the underlying PDE. We will also consider high order finite elements for differential forms, with a special attention to conforming formulations in the Sobolev spaces H(curl) and H(div).
WP2. U-FSI: Unfitted methods for Fluid-Structure Interactions (FSI)
[UNIPV, SISSA]
We plan to design, implement, and analyze unfitted methods for the approximation of PDEs modeling FSI. A relevant feature of the considered models is that they involve moving interfaces, whose position is an unknown of the problem. Our approaches include the Immersed Boundary Method (IBM), the Fictitious Domain method (FD), the CutFEM approach, as well as a recently proposed embedded method called Shifted Boundary Method (SBM).
WP3. ROM: Reduced Order Methods
[SISSA, IMATI, POLITO, UNITN]
In several applied fields, iterative optimization procedures entail successive resolution of PDEs with different values of control or design variables or different physical/geometric scenarios, thus requiring high computational efficiency. We plan to study suitable reduced order methods (ROM), such as reduced basis methods (RBM), representing an effective strategy to contain the overall computational cost. Our attention will be given to the development of ROMs relying on full order methods analysed in WP1 and WP2 (spectral methods and hp FEM, IBM, FD, CutFEM, SBM), as well as those built upon Finite Volume (FV) approximations, whose interest is growing for industrial applications.
WP4. UQ: Uncertainty Quantification, model reduction, and data
[IMATI, SISSA, POLITO]
The attention in this work package is devoted to uncertainty quantification (UQ) methods, as well as to their coupling with reduced order modelling techniques, which can be in fact a viable way to solve UQ problems at a reasonable computational cost. We will consider sampling methods for UQ, i.e., methods that solve the UQ problem by repeatedly evaluating the full/reduced model for several values of the unknown parameters, and we will tackle both forward UQ problems and inverse UQ/data assimilation problems, possibly in the challenging framework of optimization under uncertainty. On a methodological level, we will focus on developing adaptive UQ methods with respect to a) the parameterization of the uncertain quantities, b) the sampling of the parametric space and c) the spatial-temporal discretization, building on the results of WP1 and WP2. These improvements of the status-of-the-art will allow tackling relevant industrial applications.
The above methods lay the foundations for the simulation of relevant industrial and physical applications.