Breaking Integrability
“Nobody is perfect !”
--Billy Wilder
The integrable quantum field theories provide the exact solution of many statistical models away from the critical point. Despite the elegance and the undeniable success of these methods, the generic situation that occurs in statistical physics is that of a non-integrable dynamics: many interesting statistical models fall within this class and therefore it would be highly desirable to develop an appropriate formalism to deal with the lack of integrability.
This task is notoriously difficult for the rich phenomenology that arises when the dynamics is not integrable: there are decays and production scattering processes, confinement phenomena and nucleation of false vacua, resonance peaks in the cross sections, etc. All these physical aspects are usually accompanied by a great mathematical complexity. To see this, it is sufficient to consider the analytic structure of the $S$-matrix of such theories: once one has given up the integrability condition, the infinite number of thresholds of the production processes gives rise to nested patterns of branch cut singularities, in addition to the pole structure associated to the bound states or the resonances.
Quite a detailed analysis of all physical aspects of non-integrable models can be studied using the Form Factor Perturbation Theory, introduced in a paper with G. Delfino and P. Simonetti. The formalism permits to understand confinement phenomena in theory in which the breaking of integrability is realized by non-local operators with respect to the original particle excitations, as in the multiple frequency
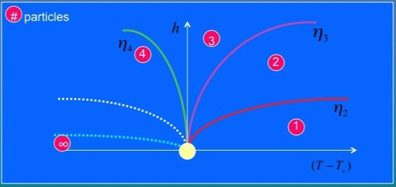
Sine-Gordon model or magnetic deformation of Ising model in its low-temperature phase. Taking advantage of the integrability of the Ising model along the pure thermal and magnetic axes, one can infer the mass spectrum evolution in the (h,T) plane.
Number of particles of the Ising model in different
regions of the (h,T) plane
The formalism can be also extended to massless theory and allows us to explain, among other things: (a) the confinement of the spinons in the O(3)-sigma model with topological term once we move away from the critical line theta=pi, and the determination of the consequent massive spectrum; (b) the mass spectrum evolution of non-integrable perturbations of minimal models of conformal field theory.
A noteworthy example of non-integrable models are obtained for supersymmetric theories, where confinement of kinks is only realized in strong-coupling regime.
In studying breaking of integrability, one can also take advantage of semi-classical methods and numerical approaches.
Main References
• G. Delfino, G. Mussardo, P. Simonetti, Non-integrable Quantum Field Theories as Perturbations of Certain Integrable Models, Nucl. Phys. B 473 (1996), 351-391, hep-th/9603011
• G. Delfino, G. Mussardo, Non-Integrable Aspects of the Multi-Frequency Sine-Gordon Model, Nucl. Phys. B 516 (1998), 675-703, hep-th/9709028
• P. Fonseca, A.B. Zamolodchikov, Ising field theory in a magnetic field: analytic properties of the free energy, J. Stat. Mech. 2003, vol. 110, no3-6, pp. 527-590, hep-th/0112167
• D. Controzzi and G. Mussardo, On the Mass Spectrum of the Two–dimensional O(3) Sigma Model with θ Term, Phys. Rev. Lett. 92 (2004), 021601, hep-th/0307143
• D. Controzzi and G. Mussardo, Mass Generation in Perturbed Massless Integrable Models, Physics Letters B 617 (2005), 133-139, hep-th/0503018
• G. Delfino, P. Grinza and Giuseppe Mussardo, Decay of particles above threshold in the Ising field theory with magnetic field, Nucl. Phys. B 737 (2006), 291-303, hep-th/0507133
• S.B. Rutkevich, Large-n excitations in the ferromagnetic Ising field theory in a small magnetic field: Mass spectrum and decay widths, Phys.Rev.Lett.95:250601,2005, hep-th/0509149
• G. Mussardo, G. Takacs, Effective potentials and kink spectra in non-integrable perturbed conformal field theories, J. Phys. A 42: 304022,2009, arXiv:0901.3537 [hep-th]
• V.A. Fateev, S.L. Lukyanov, A.B. Zamolodchikov, On mass spectrum in 't Hooft's 2D model of mesons, J.Phys.A42:304012,2009, arXiv:0905.2280 [hep-th]
• L. Lepori, G. Mussardo, G. Toth, The particle spectrum of the Tricritical Ising Model with spin reversal symmetric perturbations, J.Stat.Mech.0809:P09004,2008, arXiv:0806.4715 [hep-th]
• G. Delfino, P. Grinza, Confinement in the q-state Potts field theory, Nucl. Phys. B791: 265-283, 2008, arXiv:0706.1020
• A. Mossa, G. Mussardo, Analytic properties of the free energy: The Tricritical Ising Model, J.Stat.Mech.0803:P03010,2008, arXiv:0710.0991 [hep-th]
• G. Mussardo, Kink Confinement and Supersymmetry, JHEP 0708:003, 2007, arXi:0706.2546
• G. Brandino, R. Konik, G. Mussardo, Energy Level Distribution of Perturbed Conformal Field Theories, persymmetry, JHEP 1007 (2010), P07013.
• A. Coser, M. Beria, G. Brandino, R. Konik, G. Mussardo, Truncated Conformal Space Approach for 2D Landau-Ginzburg Theories, J. Stat. Mech. (2014) P12010
• G. Mussardo, Integrability, Non-integrability and confinement, Invited talk at StatPhys24, Cairns (Australia) 2010, J.Stat.Mech.1101:P01002,2011