Topological Quantum Computation
“Blessed is the man who loosens such a knot”
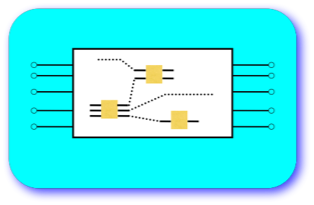
Ordinary quantum computation uses simple quantum two level systems as quantum bits (’qubits’) one- and two-qubit unitary operations serving as universal quantum gates. The main problem of such an approach is quantum decoherence, the inevitable continuous dephasing of a quantum state due to its interaction with the environment. In recent years an
interesting alternative idea has been put forward, i.e. to build a quantum computer which is topologically immune to quantum decoherence. Such an inherently fault tolerant topological quantum computer is completely protected from any local perturbation induced by the environment and uses the time-space braiding (i.e. creating suitable quantum knots) of non-Abelian anyonic quasi-particles for quantum computation.

How does topology appear in physics? It is usually an emergent property: it can be found, for instance, in fractional quantum Hall states, chiral p-wave superconductors, or rotating BEC systems. Classifying the topological phases of matter is an interesting open challenge.
Many topological states are described by topological quantum field theory, an example of which is the Chern-Simons. Topological field theories have the appealing feature to have fractional charge and statistics excitations. The ones suitable for universal quantum computation are non-abelian anyons, in particular the so-called Fibonacci anyons.
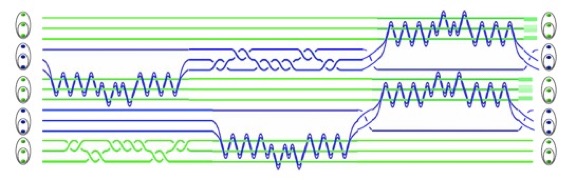
As shown by L. Hormozi, G. Zikos, N.E. Bonesteel, and S. H. Simon in the paper Topological Quantum Compling, one can use the braiding properties of the Fibonacci anyons to construct both an arbitrary SU(2) gate and a CNOT gate . These authors pursued a brute-force approach which has the merit to show the possibility of realizing such a topological quantum computation but at the price of embarking, usually, in a very large searching procedure.
Braid realization of a quantum gates
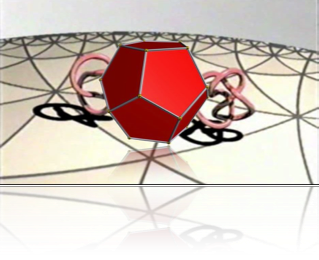
In the paper Topological Quantum Hashing with Icosahedral Group (by M. Burrello, H. Hu, G. Mussardo and X. Wan) and the next one, “Topological Quantum Gate Construction by iterative pseudogroup hasting”, we propose a very efficient algorithm to implement an arbitrary SU(2) gate with the Fibonacci
anyons. Such an algorithm relies on the group structure of the icosahedral group (the largest discrete sub-group of SU(2)) and is able to pin down the target matrix with high accuracy in less than a second on a single 3GHz CPU. To have fun with such a code, please visit the web-site braids .
Equally interesting is to study the thermodynamics of a gas of anyons (either abelian or non-abelian) and extract the virial coefficients which encode the interactions of those systems. One can obtain in this way the main thermodynamical quantities at the lower order of the virial expansion. Moreover, one can also extract statistical interparticle potential of an ideal system of non-Abelian Chern-Simons (NACS) particles and compare it with the corresponding results of an ideal gas of Abelian anyons. Studying the equation of state of Abelian anyons and non-Abelian Chern-Simons particles, one can see the energy is just proportional to the pressure, with the proportionality constant being simply the area of the system. Soft-core boundary conditions at coincident points for the two-body wavefunction of anyons introduce a length scale, and induce a non-vanishing internal energy shift: for such boundary conditions the energy-pressure ratio does not match the area of the system, opposed to what happens for hard-core (and in particular 2d Bose and Fermi) ideal anyonic gases.
Relevant publications
• M. Burrello, X. Hu, G. Mussardo, X. Wan, Topological Quantum Hashing with the Icosahedral Group, http://arxiv.org/pdf/0903.1497, Phys. Rev. Lett. 104, 160502 (2010)
• M. Burrello, X. Hu, G. Mussardo, X. Wan, Topological Quantum Gate Construction by iterative pseudogroup hasting, New Journal of Physics 13 (2011), 025023
• F. Mancarella, G. Mussardo, A. Trombettoni, Statistical Mechanics of an Ideal Gas of non-Abelian Anyons, Nucl. Phys. B867, (2013), 950.
• F. Mancarella, G. Mussardo, A. Trombettoni, Statistical Interparticle Potential of an Ideal Gas of non-Abelian Anyons, J. Phys. A46, (2013), 275001.
• F. Mancarella, G. Mussardo, A. Trombettoni, Energy-pressure relation for low-dimensional gases, Nucl. Phys. B 887, (2014), 216.
Main References
• A. Kitaev, Anyons in an exactly solvable model and beyond, Annals of Physics, 321, 2 (2006), arXiv:cond-mat/0506438
• S. Das Sarma, M. Freedman, C. Nayak, S.H. Simon, A. Stern, Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80, 1083 (2008), arXiv:0707.1889
• S. Das Sarma, M. Freedman, C. Nayak, Topological Quantum Computation, Physics Today 59, Issue 7, 32 (2006).
• J. Preskill, Topological Quantum Computation, download .
• S. Trebst, M. Troyer, Z. Wang, A.W.W. Ludwig, A short introduction to Fibonacci Anyons, Progress of Theor. Phys. Supplement 176, 384 (2008), arXiv:0902.3275
• L. Hormozi, G. Zikos, N.E. Bonesteel, S.H. Simon, Topological Quantum Compiling, Phys. Rev. B 75 (2007), 165310, arXiv:quant-ph/0610111