Out of Equilibrium
“That kick, at Madison Square Garden that night, was really a dramatic blow”
Primo Carnera

Equilibrium is a rather ideal situation, the exception rather than the rule in Nature. Instead, most physical systems are out of equilibrium. The understanding and theoretical description of far from equilibrium systems poses one of the major present challenges in theoretical physics.
Out of equilibrium physical situations are manifold. On the one hand, whenever the external or internal parameters of a physical
system are varied its subsequent relaxation to equilibrium under the new conditions may be either impossible or take very long times. A classical instance of the latter is the « quench » of a macroscopic system to its thermal critical point or across it. Quantum protocols of this kind can now be realized with relatively large cold atom systems. On the other hand, the evolution of numerous physical systems at very different scales involves transport of mass, energy, charge, etc., not compatible with equilibrium. A quantum case is electronic transport through ever-smaller nano-structures, even single molecules. Traditional examples for which a classical description is sufficient are heat conduction and fluid flow. All these situations are interesting and admit experimental realizations of practical interest but have not been fully understood and pose hard theoretical problems.
In recent years, in particular due to outstanding experimental advances in quantum devices and cold atomic physics, we have witnessed the opening of a new chapter in Physics, which covers Quantum Physics, Statistical Physics and Mathematical Physics. These experimental advances have led to a resurgence of interest in fundamental questions of quantum statistical physics and classical statistical physics as well. Key theoretical question in this context are: How does an isolated many-body quantum system relax? Which physical principles underlie the relaxation and what are the associated timescales? What characterizes the steady states reached at late times? How can one quantify and characterize dissipative effects? What is the role played by impurities and quenched disorder?
Questions on the equilibration mechanisms of closed macroscopic classical systems have been posed in the past, especially in the first half of the 20th century. They are known to be very difficult to answer and (to a certain extent) they have been left aside by the statistical physics community. Instead, focus in statistical physics research has been set on the dynamics of dissipative (open) many-body classical systems and their possible slow out of equilibrium relaxation due to competing interactions or quenched randomness. A huge amount of knowledge gained in this area remains unconnected from the questions posed in the quantum context.
Many facets of the subject have come into focus in recent years, because theoretical ideas or new models can be tested either by numerical methods or directly by designed experiments. A precise protocal is given by the so-called Quantum Quench: consider a quantum system initially prepared in the ground state |B> of a Hamiltonian H(g0). At the time t=0, the coupling constant g is abruptly changed from the initial value g0 to the new value g1. This process is a quantum quench, a swift kick to the system. The abrupt change of the Hamiltonian leads the system out of equilibrium but its subsequent time evolution is perfectly unitary and ruled by the new Hamiltonian H(g1).
If the system has few degrees of freedom, the time evolution is very well understood and the expectation values of the various observables on the initial state |B> presents, in general, a periodic (or quasi-periodic) behaviour. This quantum recurrence simply comes from the decomposition of the initial state |B> in terms of the energy eigenvectors of the new Hamiltonian: for the new Hamiltonian, |B> is in fact an excited state and, since the energy is conserved, the system cannot relax to the new ground state: imagine, for instance, a quantum oscillator in its initially ground state once the elastic coupling of the Hamiltonian is suddendly changed.
The previous scenario changes, however, if the quantum system has infinitely many degrees of freedom. In this case, one can imagine that, for any given sub-system, the rest of the sample acts as a thermal bath and therefore the situation is less clear.
Does an extended quantum system reach asymptotically a stationary state after a quench? If so, does it keep memory of the initial state |B> or it assume a thermal form? For long time, these were considered purely theoretical questions, because for any extended quantum systems coupling to enviroment were considered unavoidable, with the subsequent thermalization due to decoherence and dissipation. But, in cold atom set-ups these effects can be largely minimised, even elimininate at all! Therefore, the topic has become an active and rapid developing field of research for a large community of scientists, ranging from quantum optics to integrable models.
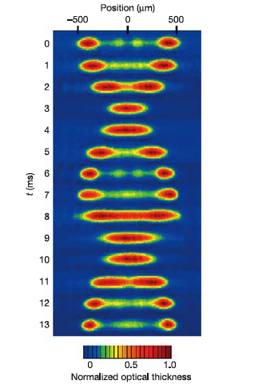
Oscillations of cold atoms after a quench
from T. Kinoshita et al. (Nature)
Modern techiques of analysis involve Boundary Conformal Theory, Boundary Integrable Field Theory, Exact Diagonalization and Density Matrix Renormalization Group.
One of the important question is whether integrability plays any role in determining the large-time evolution. This question has been addressed by several authors and it has been the subject of a series of papers which I wrote in collaboration with A. De Luca, D. Fioretto, F. Essler, M. Panfil, D. Rossini, G. Santoro and A. Silva.
Relevant Publications
• D. Rossini, A. Silva, G. Mussardo, G. Santoro, Effective Thermal Dynamics Following a Quantum Quench in a Spin Chain, Phys. Rev. Lett. 102, 127204 (2009) arXiv:0810.55082002
• D. Rossini, S. Susuki, G. Mussardo, G. Santoro, A. Silva, Long time dynamics following a quench in an integrable quantum spin chain: local versus non-local operators and effective thermal behavior, Phys. Rev. B 82, 144302 (2010)
• D. Fioretto, G. Mussardo, Quantum Quenches in Integrable Field Theories, New Journal of Physics 12: 055015 (2010), arXiv:0911.3345
• S. Sotiriadis, D. Fioretto, G. Mussardo, Zamolodchikov-Faddev Algebra and Quantum Quench in Integrable Quantum Field Theories, JSTAT (2012), P02017
• G. Brandino, A. De Luca, R. Konik, G.. Mussardo, Quench Dynamics in Randomly Generated Extended Quantum Mechanics, Phys. Rev. B 85, 214435 (2012)
• G. Mussardo, Infinite Time Average of Local Fields in an Integrable Quantum Field Theory, Phys. Rev. Lett. 111 (2013), 100401
• S. Sotiriadis, G. Takacs, G. Mussardo, Boundary State in an Integrable Quantum Field Theory Out of Equilibriumg time dynamics following a quench, Phys. Lett. B 734 (2014) 52
• F. Essler, G. Mussardo, M. Panfil, Generalized Gibbs Ensembles for Quantum Field Theories, Phys. Rev. A91 (2015), 051602
• A. C. Cubero, G. Mussardo, M. Panfil, Quench Dynamics in Two-dimensional Integrable SUSY Models, JSTAT 1603 (2016), 033115
• A. De Luca, G. Mussardo, Equilibration Properties of Classical Integrable Field Theories, JSTAT 1612 (2016), n. 12, 123104
• F. Essler, G. Mussardo, M. Panfil, On truncated generalized Gibbs ensembles in Ising field theory, JSTAT 1701 (2017), n. 1, 013103.
Main References
• M. Greiner, O. Mandel, T. W. H¨ansch, and I. Bloch, Collapse and Revival of the Matter Wave Field of a Bose-Einstein Condensate, 2002 Nature (London) 419 51, cond-mat/0207196
• T. Kinoshita, T. Wenger, and D. S. Weiss, A quantum Newton’s cradle, 2006 Nature 440, 900
• P. Calabrese, J.L. Cardy, Quantum Quenches in Extended Systems, J. Stat. Mech. (2007) P10004, arXiv:0708.3750.
• S. Ghoshal, A.B. Zamolodchikov, Boundary S matrix and boundary state in two-dimensional integrable quantum field theory, Int. J. Mod. Phys. A9 (1994) 3841--3886 [ Erratum-ibid. A A9, (1994) 4353] hep-th/9306002].
• M. Rigol, V. Dunjko, M. Olshanii, Thermalization and its mechanics for generic isolated systems, Nature 452 (2008), 854.
• A. Polkovnikov, K. Sengupta, A. Silva and M. Vengalattore, Rev. Mod. Phys. 83, 863-883 (2011)
• Special issue on Quantum Integrability in Out of Equilibrium Systems, editors P. Calabrese, F.H.L. Essler and G. Mussardo, J. Stat. Mech. (2016) 064001