Finite Size and Temperature

A series of new information on quantum systems with infinite degrees of freedom or statistical models can be obtained by studying their behavior on a finite geometry. Typical geometrical configurations are: (a) a semi-infinite plane, i.e. a system with one boundary; (b) a strip, i.e. a system with two boundaries; (c) a cylinder, i.e. a system with periodic boundary conditions.

When a two-dimensional system is at its critical point, as shown in particular by J. Cardy, all the effects coming from the finite size of the system can be controlled by the underlying Conformal Field Theory. So, one can compute the exact expression of the partition functions in presence of different boundary conditions, the relative operator content, the entropy of the boundaries and

various correlation functions of the order parameters.

A key concept in this context is the definition of Boundary State |B>: this is a particular state of the bulk theory which encodes all information about the boundary condition. As the BCS state in superconductivity, the boundary state is made of an infinite number of particle pairs: this ensures that no-energy flow crosses the boundary of the system. The boundary state formalism plays an important role in the analysis of quantum quenches, since the boundary state is nothing else but the state in which the system is initially prepared. The entropy of the boundary states enters the so-called g-function, that is conjectured satifies a monotonous decreasing behaviour under the Renormalization Group flow.

As shown by S. Ghoshal and A. Zamolodchikov, the notion of boundary state can be naturally generalized to massive Integrable Field Theory. In this case we even get additional information: in fact, the amplitude of the virtual emission of each particle pair can be directly related to reflection scattering amplitude of the quasi-particles in the crossing channel, i.e. in the system the role of space and time axes has been swapped.

In integrable field theoris, using the boundary states, one can compute not only partition functions

with different boundary conditions but also the

correlators of the order parameters.

Trying to extend the formalism to theories with defect lines, one faces a no-go theorem: in fact, as shown by G. Delfino, G. Mussardo and P. Simonetti, the only massive integrable theories with integrable defect are the quasi-free theories, among which there is the two-dimensional Ising model. This is the result of implementing a Yang-Baxter equation involving both the transmission and the reflection amplitudes.

The cylinder geometry allows us to deal with finite-temperature effects. For integrable quantum field theories, as shown by Al.B. Zamolodchikov the partition function can be exactly computed generalizing to the relativistic case the Thermodynamic Bethe Ansatz equations derived by Yang and Yang. Swapping the role of space and time axes, in this case one gets information on the finite-volume ground state energy, i.e. on the Casimir effect. A proposal to compute correlation functions of integrable field theory at a finite temperature has been put forward by A. LeClair and G. Mussardo and has passed, for the one-point functions, several checks of consistency. This formalism has been used to compute the one-point functions of Lieb-Liniger cold atom gas using the Form Factors of the Sinh-Gordon model.

There is a simple but very effective idea to study energy levels of a quantum field theory on a finite geometry: V.P. Yurov and Al.B. Zamolodchikov proposed, in fact, to use the conformal basis of the states (truncated at a certain level of their Verma modules) to implement an effective Hamiltonian for massive deformations of critical point hamiltonians. This research program can be efficiently carried on with the help of a computer program, which builds the truncated Hilbert space and computes the matrix elements of the deforming operators.

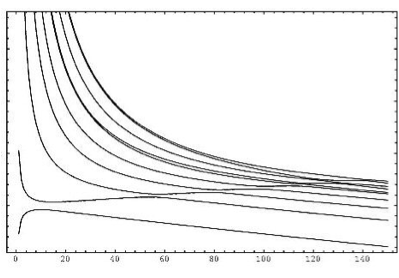
Energy levels of Ising model in magnetic field at

low-temperatures, as functions of the width R of

the cylinder geometry.

The Truncated Conformal Space Approach (TCSA) has proved to be a valid alternative to Montecarlo simulations, being closer to a transfer matrix approach. Among its many advantages, it worth mentioning that it does not rely on integrable properties of the Hamiltonian under scrutiny: integrabilty and its breaking can be rather inferred from the pattern of the crossing or the repulsions of the energy levels. TCSA has permitted to study highly non-perturbative effects, e.g. the decay of false vacua, properties of resonances, matrix elements of order parameters, three-point couplings, level statistics for integrable and non-integrable theories. TCSA (and Renormalization Group refinement) provides an efficient way to investigate the energy level distribution of integrable and non-integrable deformations of CFT’s.

Main Publications

• M. Lassig, G. Mussardo, J.L. Cardy, The Scaling Region of the Tricritical Ising Model in Two Dimensions, Nucl. Phys. B 348 (1991), 591-618.

• M. Lassig, G. Mussardo, Hilbert Space and Structure Constants of Descendant Fields in

Two-dimensional Conformal Theories, Computer Physics Communications. 66 (1991), 71-88.

• R. Konik, A. LeClair and G. Mussardo, On Ising Correlation Functions with Boundary Magnetic Field, Int. J. Mod. Phys. A 11 (1996), 2765-2782, hep-th/9508099

• G. Delfino, G. Mussardo and P. Simonetti, Scattering Theory and Correlation Functions in Statistical Models with a Line of Defect, Nucl. Phys. B 432 (1994), 518-550, hep-th/9409076

• A. LeClair, G. Mussardo, H. Saleur, S. Skorik, Boundary energy and boundary states in integrable quantum field theories, Nucl.Phys.B453:581-618,1995. hep-th/9503227

• A. LeClair, G. Mussardo, Finite Temperature Correlation Functions in Integrable QFT

Nucl.Phys. B 552 (1999), 624-642. hep-th/9902075

• G. Mussardo, On the Finite Temperature Formalism in Integrable Quantum Field Theories

Journ. Phys. A 34 (2001), 7399-7410. hep-th/0103214

• G. Mussardo, V. Riva and G. Sotkov, Finite Volume Form–Factors in Semiclassical Approximation, Nucl. Phys. B 670 (2003), 464–478, hep-th/0307125

• G. Mussardo, G. Takacs, Effective potentials and kink spectra in non-integrable perturbed conformal field theories, J.Phys.A42:304022,2009, arXiv:0901.3537 [hep-th]

• G. Brandino, R. Konik, G. Mussardo, Energy level distribustion of perturbed conformal field theories, arXiv:1004.4844 [cond-mat.stat-mech]

• L. Lepori, G. Mussardo, G. Toth, The particle spectrum of the Tricritical Ising Model with spin reversal symmetric perturbations, J. Stat. Mech. 0809:P09004,2008, arXiv:0806.4715 [hep-th]

• A. Mossa and G. Mussardo, Analytic Properties of the Free Energy: the Tricritical ising Model,

J. Stat.Mech.0803:P03010,2008, arXiv:0710.0991 [hep-th]

• P. Mosconi, G. Mussardo, V. Riva, Boundary Quantum Field Theories with Infinite Resonance States, Nucl. Phys. B 621 (2002), 571-586, hep-th/0107082

• A. De Martino, M. Moriconi, G. Mussardo, Reflection Scattering Matrix of the Ising Model in a Random Boundary Magnetic Field, Nucl. Phys. B 509 (1998) 615-636

• G. Delfino, G. Mussardo and P. Simonetti, Statistical Models with a Line of Defect, Phys. Lett. B 328 (1994), 123-129, hep-th/9403049

• D. Fioravanti, G. Mussardo and P. Simon, Universal Amplitude Ratios of the Renormalization Group: Two–Dimensional Tricritical Ising Model, Phys. Rev. E 63 (2001), 016103, cond-mat/0008216

• D. Fioravanti, G. Mussardo and P. Simon, Universal Ratios in the 2D Tricritical Ising Model, Phys.Rev.Lett.85:126-129,2000, hep-th/0002225

Main References

J.L. Cardy, Boundary conformal field theory, in Encyclopedia of Mathematical Physics (2004), hep-th/0411189

S. Ghoshal and A.B. Zamolodchikov, Boundary S matrix and boundary state in two-dimensional

integrable quantum field theory, Int.J.Mod.Phys.A9:3841-3886,1994, Erratum-ibid.A9:4353,1994. hep-th/9306002

• C.N. Yang, C.P. Yang, Thermodynamics of one-dimensional system of bosons with repulsive delta-function interaction, Journ. Math. Phys. 10, 1. 1115 (1969)

Al.B. Zamolodhikov, Thermodynamic Bethe Ansatz In Relativistic Models. Scaling Three State Potts And Lee-Yang Models, Nucl.Phys.B342:695-720,1990.

V.P. Yurov and Al.B. Zamolodchikov, Truncated Conformal Space Approach To Scaling Lee-Yang Model, Int.J.Mod.Phys.A5:3221-3246,1990

S.L. Lukyanov, Finite temperature expectation values of local fields in the sinh-Gordon model, Nucl.Phys.B612:391-412,2001, hep-th/0005027